
(1)求点C的轨迹C的方程;
(2)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设![]() ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线J的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线J的方程;若不存在,试说明理由.
解:(1) Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN![]() GQ为PN的中垂线
GQ为PN的中垂线![]() |PG|=|GN|
|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故C点的轨迹是以M、N为焦点的椭圆,其长半轴长a=3,半焦距c=![]() ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是![]() =1
=1
(2)因为![]() ,所以四边形OASB为平行四边形.若存在l使得
,所以四边形OASB为平行四边形.若存在l使得![]() ,则四边形OASB为矩形
,则四边形OASB为矩形
∴![]() =0,
=0,
若l的斜率不存在,直线l的方程为x=2,
由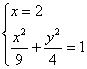 得
得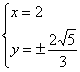
∴![]() =
=![]() >0,与
>0,与![]() =0矛盾,故l的斜率存在.
=0矛盾,故l的斜率存在.
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
由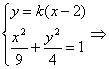 (9k2+4)x2-36k2x+36(k2-1)=0
(9k2+4)x2-36k2x+36(k2-1)=0
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ①
①
y1y2=[k(x1-2)][k(x2-2)]
k2[x1x2-2(x1+x2)+4]=![]() ②
②
把①,②代入x1x2+y1y2=0得k=±![]()
∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等.


科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 9r2 |
| 4 |
| PQ |
| QN |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 5 |
| NP |
| NQ |
| GQ |
| NP |
| OS |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 5 |
| NP |
| NQ |
| GQ |
| NP |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)(理22(1)文21(1))求点G的轨迹C的方程;
(2)(理22(2))过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设![]() ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程,若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程,若不存在,试说明理由.
(文21(2))直线l的方程为l:3x-2y-6=0,与曲线C交于A、B两点,O是坐标原点,且![]() ,求证:四边形OASB为矩形.
,求证:四边形OASB为矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com