
分析 (1)l利用等差数列与等比数列的通项公式可得an,再利用递推关系可得bn.
(2)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)∵a1,a3,a2+14成等差数列,∴2a3=a1+a2+14,a1=1,
∴2q2=1+q+14,q>1,解得q=3,
∴an=3n-1.
∵数列{bn}满足:a1b1+a2b2+…+anbn=(n-1)•3n+1,n∈N.
∴n=1时,a1b1=1,∴b1=1.
n≥2时,a1b1+a2b2+…+an-1bn-1=(n-2)•3n-1+1,
∴anbn=(2n-1)•3n-1.
∴bn=2n-1.
(2)$\frac{{b}_{n}}{{a}_{n}}$=$\frac{2n-1}{{3}^{n-1}}$.
∴数列$\{\frac{b_n}{a_n}\}$的前n项和Tn=1+$\frac{3}{3}$+$\frac{5}{{3}^{2}}$+…+$\frac{2n-1}{{3}^{n-1}}$.
$\frac{1}{3}{T}_{n}$=$\frac{1}{3}$+$\frac{3}{{3}^{2}}$+…+$\frac{2n-3}{{3}^{n-1}}$+$\frac{2n-1}{{3}^{n}}$,
∴$\frac{2}{3}{T}_{n}$=1+2$(\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n-1}})$-$\frac{2n-1}{{3}^{n}}$=1+2×$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$-$\frac{2n-1}{{3}^{n}}$,
∴${T_n}=3-\frac{n+1}{{{3^{n-1}}}}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
已知a>0,b>0,且2a+b=ab,则a+2b的最小值为( )
A.5+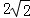 B.
B. C.5 D.9
C.5 D.9
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,0) | C. | (-∞,0),(0,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
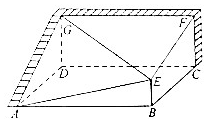 要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.
要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
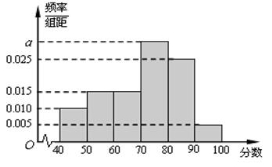
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: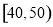 ,
,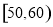 ,…,
,…,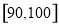 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(Ⅰ)求分数在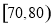 内的频率;
内的频率;
(Ⅱ)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(Ⅲ)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{16}{5}$ | C. | 2$\sqrt{41}$ | D. | 164 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com