
分析 根据函数的奇偶性求出f(x)的解析式,令t=f(x),将方程转化为一元二次函数,由根与系数之间的关系进行求解即可.
解答 解:设x<0,则-x>0,满足表达式f(x)=x|x-2|.
∴f(-x)=-x|-x-2|=-x|x+2|,
又∵f(x)为偶函数,∴f(-x)=f(x),
∴f(x)=-x|x+2|,
故当x<0时,f(x)=-x|x+2|.
则f(x)=$\left\{\begin{array}{l}{x|x-2|,}&{x≥0}\\{-x|x+2|,}&{x<0}\end{array}\right.$,
作出f(x)的图象如图:
设t=f(x),
由图象知,当t>1时,t=f(x)有两个根,
当t=1时,t=f(x)有四个根,
当0<t<1时,t=f(x)有六两个根,
当t=0时,t=f(x)有三个根,
当t<0时,t=f(x)有0个根,
则方程[f(x)]2+af(x)+b=0等价为t2+at+b=0,
若方程[f(x)]2+af(x)+b=0(a∈R)恰好有1个不同实数解,
等价为方程t2+at+b=0有两不同的根,
且0<t1<1,t2=1,
则t1+t2=-a,
即1<t1+t2<2,
则1<-a<2,
即-2<a<-1,
则a的取值范围为(-2,-1),
故答案为:(-2,-1)
点评 本题考查函数的单调性和奇偶性的运用,主要考查方程与函数的零点的关系,利用换元法转化为一元二次方程根与系数之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,2) | C. | (0,$\frac{1}{6}$)∪(1,+∞) | D. | (0,$\frac{1}{6}$)∪(1,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
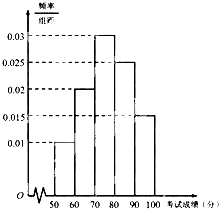 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com