
【题目】下列关于空间向量的命题中,正确的有______.
①若向量![]() ,
,![]() 与空间任意向量都不能构成基底,则
与空间任意向量都不能构成基底,则![]() ;
;
②若非零向量![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,则有
,则有![]() ;
;
③若![]() ,
,![]() ,
,![]() 是空间的一组基底,且
是空间的一组基底,且![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
④若向量![]() ,
,![]() ,
,![]() ,是空间一组基底,则
,是空间一组基底,则![]() ,
,![]() ,
,![]() 也是空间的一组基底.
也是空间的一组基底.
 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,椭圆
的一个焦点重合,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,记直线
上一点,记直线![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() 和
和![]() ,且满足
,且满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: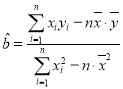 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国.根据环保部门对某河流的每年污水排放量![]() (单位:吨)的历史统计数据,得到如下频率分布表:
(单位:吨)的历史统计数据,得到如下频率分布表:

将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(1)求在未来3年里,至多1年污水排放量![]() 的概率;(2)该河流的污水排放对沿河的经济影响如下:当
的概率;(2)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元.为减少损失,现有三种应对方案:
时,经济损失为60万元.为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费3.8万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种文案,哪种方案好,并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,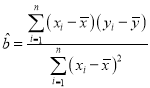
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司准备在2020年年初将两千万投资东营经济开发区的“示范区”新型物流,商旅文化两个项目中的一个之中.
项目一:新型物流仓是为企业提供仓储、运输、配送、货运信息等综合物流服务的平台.现准备投资建设10个新型物流仓,每个物流仓投资0.2千万元,假设每个物流仓盈利是相互独立的,据市场调研,到2022年底每个物流仓盈利的概率为![]() ,若盈利则盈利为投资额的40%,否则盈利额为0.
,若盈利则盈利为投资额的40%,否则盈利额为0.
项目二:购物娱乐广场是一处融商业和娱乐于一体的现代化综合服务广场.据市场调研,投资到该项目上,到2022年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为![]() 和
和![]() .
.
(1)若投资项目一,记![]() 为盈利的物流仓的个数,求
为盈利的物流仓的个数,求![]() (用
(用![]() 表示);
表示);
(2)若投资项目二,记投资项目二的盈利为![]() 千万元,求
千万元,求![]() (用
(用![]() 表示);
表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com