
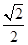 AB.
AB.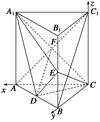
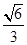
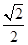 AB得,AC⊥BC.以C为坐标原点,
AB得,AC⊥BC.以C为坐标原点,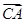 的方向为x轴正方向,
的方向为x轴正方向,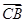 的方向为y轴正方向,
的方向为y轴正方向,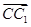 的方向为z轴正方向,建立如图所示的空间直角坐标系C-xyz.设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),
的方向为z轴正方向,建立如图所示的空间直角坐标系C-xyz.设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),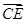 =(1,1,0),
=(1,1,0),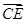 =(0,2,1),
=(0,2,1),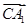 =(2,0,2).
=(2,0,2).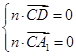 即
即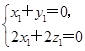 可取n=(1,-1,-1).
可取n=(1,-1,-1).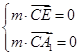 即
即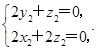 可取m=(2,1,-2).
可取m=(2,1,-2). 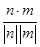 =
=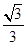 ,故sin〈n,m〉=
,故sin〈n,m〉=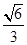


科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
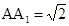 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.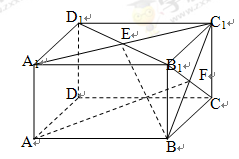
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
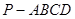 中,底面
中,底面 为菱形,
为菱形,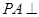 平面
平面 ,
,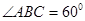 ,
,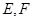 分别是
分别是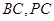 的中点.
的中点.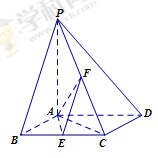
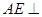 平面
平面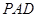 ;
;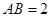 ,若
,若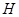 为
为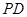 上的动点,
上的动点,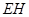 与平面
与平面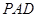 所成最大角的正切值为
所成最大角的正切值为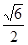 ,求二面角
,求二面角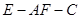 的余弦值。
的余弦值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
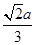 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).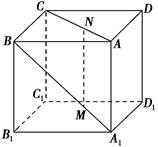
| A.相交 | B.平行 | C.垂直 | D.不能确定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
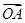 =
=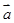 ,
,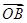 =
=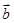 ,其中
,其中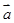 =(3,1),
=(3,1),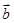 =(1,3).若
=(1,3).若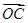 =λ
=λ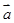 +μ
+μ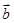 ,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表示正确的是( )
,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表示正确的是( )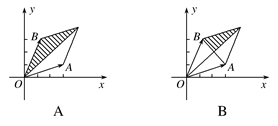
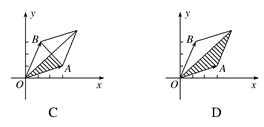
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com