练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设f（x）=|x﹣3|+|x﹣4|．
    （1）求函数 的定义域；
    （2）若存在实数x满足f（x）≤ax﹣1，试求实数a的取值范围．

    【答案】
    （1）解：∵ ，

    它与直线y=2交点的横坐标为 和 ．

    ∴不等式 的定义域为


    （2）解：函数y=ax﹣1的图象是过点（0，﹣1）的直线，

    作出图象，如下图：

    结合图象可知，a取值范围为


    【解析】（1）求出f（x）=|x﹣3|+|x﹣4|与直线y=2交点的横坐标为 和 ，由此能求出不等式 的定义域．（2）函数y=ax﹣1的图象是过点（0，﹣1）的直线，作出图象，结合图象能求出实数a的取值范围．
    【考点精析】掌握绝对值不等式的解法是解答本题的根本，需要知道含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD=2，P为平面ABCD外一点，且PB⊥BD．
    （1）求证：PA⊥BD；
    （2）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD；
    （3）若PC⊥CD，PB=4，求四棱锥P﹣ABCD的体积．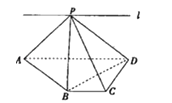

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某住宅小区的平面图呈圆心角为的扇形，小区的两个出入口设置在点及点处，且小区里有一条平行于的小路。

    （1）已知某人从沿走到用了分钟，从沿走到用了分钟，若此人步行的速度为每分钟米，求该扇形的半径的长（精确到米）

    （2）若该扇形的半径为，已知某老人散步，从沿走到，再从沿走到，试确定的位置，使老人散步路线最长。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE、BE，∠APE的平分线与AE、BE分别交于点C、D，其中∠AEB=30°．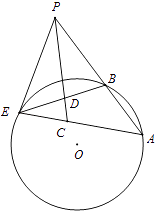

    （1）求证：
    （2）求∠PCE的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年，河北等8省公布了高考改革综合方案将采取“3+1+2”模式，即语文、数学、英语必考，然后考生先在物理、历史中选择1门，再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划，甲同学对高一一年来的七次考试成绩进行统计分析，其中物理、历史成绩的茎叶图如图所示.

    (1)若甲同学随机选择3门功课，求他选到物理、地理两门功课的概率；

    (2)试根据茎叶图分析甲同学应在物理和历史中选择哪一门学科？并说明理由；

    (3)甲同学发现，其物理考试成绩(分)与班级平均分(分)具有线性相关关系，统计数据如下表所示，试求当班级平均分为50分时，其物理考试成绩.

    参考数据: ，，，.

    参考公式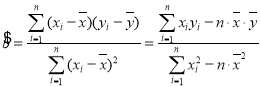：，，(计算时精确到).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE、BE，∠APE的平分线与AE、BE分别交于点C、D，其中∠AEB=30°．

    （1）求证：
    （2）求∠PCE的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为、，过的直线与椭圆交于、两点，若是以为直角顶点的等腰直角三角形，则椭圆的离心率为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的左、右焦点分别为、，是双曲线上一点，且轴，若的内切圆半径为，则其渐近线方程是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=emx﹣lnx﹣2．
    （1）若m=1，证明：存在唯一实数t∈（ ，1），使得f′（t）=0；
    （2）求证：存在0＜m＜1，使得f（x）＞0．

    查看答案和解析>>

    同步练习册答案