Question

 设f(x)、g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)·g(x)＋f(x)·g′(x)＞0，且f(－3)·g(－3)＝0，则不等式f(x)·g(x)＜0的解集是(  )

A．(－3,0)∪(3，＋∞)             

B．(－3,0)∪ (0,3)

C．(－∞，－3)∪(3，＋∞)        

D．(－∞，－3)∪(0,3)

 

Answer 1

【答案】

D

【解析】

试题分析：设F（x）=f （x）g（x），当x＜0时，∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0．∴F（x）在当x＜0时为增函数．

∵F（-x）=f （-x）g （-x）=-f （x）•g （x）=-F（x）．

故F（x）为（-∞，0）∪（0，+∞）上的奇函数．

∴F（x）在（0，∞）上亦为增函数．

已知f(－3)·g(－3)＝0，必有F（-3）=F（3）=0．

构造如图的F（x）的图象，

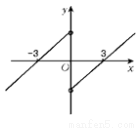
可知F（x）＜0的解集为x∈（-∞，-3）∪（0，3）．

考点：本试题主要考查了复合函数的求导运算和函数的单调性与其导函数正负之间的关系．

点评：导数是一个新内容，也是高考的热点问题，要多注意复习．解决该试题的关键是先根据f’（x）g（x）+f（x）g’（x）＞0可确定[f（x）g（x）]'＞0，进而可得到f（x）g（x）在x＜0时递增。