
【题目】已知函数f(x)=(ax﹣1)lnx+ ![]() . (Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线l的方程;
. (Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线l的方程;
(Ⅱ)设函数g(x)=f'(x)有两个极值点x1 , x2 , 其中x1∈(0,e),求g(x1)﹣g(x2)的最小值.
【答案】解:(I)当a=2时, ![]() ,
,
得切线l的方程为 ![]() 即4x﹣2y﹣3=0.
即4x﹣2y﹣3=0.
(II) ![]() ,定义域为(0,+∞),
,定义域为(0,+∞),
![]() ,令g'(x)=0得x2+ax+1=0,
,令g'(x)=0得x2+ax+1=0,
其两根为x1,x2,且x1+x2=﹣a,x1x2=1,
故 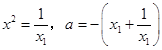 .
.
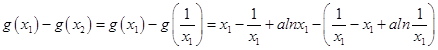
= 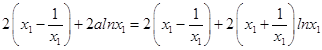 ,
,
![]() .
.
则(g(x1)﹣g(x2))min=h(x)min, ![]() ,
,
当x∈(0,1]时,恒有h'(x)≤0,x∈(1,e]时,恒有h'(x)<0,
总之当x∈(1,e]时,h(x)在x∈(0,e]上单调递减,
所以 ![]() ,
,
∴ ![]() .
.
【解析】(Ⅰ)求出函数的导数,计算f(1),f′(1),求出切线方程即可;(Ⅱ)求出函数的导数,得到 ![]() ,求出g(x1)﹣g(x2)的解析式,根据函数的单调性求出其最小值即可.
,求出g(x1)﹣g(x2)的解析式,根据函数的单调性求出其最小值即可.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两个容器,甲容器容量为x,装满纯酒精,乙容器容量为z,其中装有体积为y的水(x,y<z,单位:L).现将甲容器中的液体倒入乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒入甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过n(n∈N*)次操作之后,乙容器中含有纯酒精an(单位:L),下列关于数,列{an}的说法正确的是( )
A.当x=y=a时,数列{an}有最大值 ![]()
B.设bn=an+1﹣an(n∈N*),则数列{bn}为递减数列
C.对任意的n∈N* , 始终有 ![]()
D.对任意的n∈N* , 都有 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列{an}同时满足下列条件: ①a1=m(m∈N*);②an≤n﹣1(n≥2);③n是a1+a2+…+an的因数(n≥1).
(Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)若数列{an}的前三项互不相等,且n≥3时,an为常数,求m的值;
(Ⅲ)求证:对任意正整数m,存在正整数M,使得n≥M时,an为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤ ![]() )的部分图象如图所示,若方程f(x)=a在x∈[﹣
)的部分图象如图所示,若方程f(x)=a在x∈[﹣ ![]() ,
, ![]() ]上有两个不相等的实数根,则a的取值范围是( )
]上有两个不相等的实数根,则a的取值范围是( ) 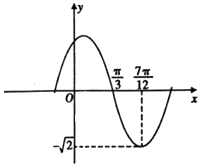
A.[ ![]() ,
, ![]() )
)
B.[﹣ ![]() ,
, ![]() )
)
C.[﹣ ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2=
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2= ![]() ,且直线l经过曲线C的左焦点F. ( I )求直线l的普通方程;
,且直线l经过曲线C的左焦点F. ( I )求直线l的普通方程;
(Ⅱ)设曲线C的内接矩形的周长为L,求L的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() =1(a>b>0)焦点的直线x+y﹣2
=1(a>b>0)焦点的直线x+y﹣2 ![]() =0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
=0交M于P,Q两点,G为PQ的中点,且OG的斜率为9.
(1)求M的方程;
(2)A、B是M的左、右顶点,C、D是M上的两点,若AC⊥BD,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合 ![]() ,定义了一种运算“
,定义了一种运算“ ![]() ”,使得集合
”,使得集合 ![]() 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素 ![]() ,使得对任意
,使得对任意 ![]() ,都有
,都有 ![]() ,则称元素
,则称元素 ![]() 是集合
是集合 ![]() 对运算“
对运算“ ![]() ”的单位元素.例如:
”的单位元素.例如: ![]() ,运算“
,运算“ ![]() ”为普通乘法;存在
”为普通乘法;存在 ![]() ,使得对任意
,使得对任意 ![]() ,都有
,都有 ![]() ,所以元素
,所以元素 ![]() 是集合
是集合 ![]() 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“ ![]() ”:
”:
② ![]() ,运算“
,运算“ ![]() ”为普通减法;
”为普通减法;
② ![]() 表示
表示 ![]() 阶矩阵,
阶矩阵, ![]() },运算“
},运算“ ![]() ”为矩阵加法;
”为矩阵加法;
③ ![]() (其中
(其中 ![]() 是任意非空集合),运算“
是任意非空集合),运算“ ![]() ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“ ![]() ”有单位元素的集合序号为( )
”有单位元素的集合序号为( )
A.①②;
B.①③;
C.①②③;
D.②③.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com