
已知函数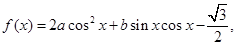 x∈R且
x∈R且 ,
,
(Ⅰ)求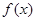 的最小正周期;
的最小正周期;
(Ⅱ)函数f(x)的图象经过怎样的平移才能使所得图象对应的函数成为偶函数?(列举出一种方法即可).
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:走向清华北大同步导读·高一数学·上 题型:013
已知函数![]() (x∈R且x≠1),那么它的反函数为
(x∈R且x≠1),那么它的反函数为
[ ]
A.![]() (x∈R,且x≠1)
(x∈R,且x≠1)
B.![]() (x∈R,且x≠6)
(x∈R,且x≠6)
C.![]() (x∈R,且x≠
(x∈R,且x≠![]() )
)
D.![]() (x∈R,且x≠-5)
(x∈R,且x≠-5)
查看答案和解析>>
科目:高中数学 来源:浙江省模拟题 题型:解答题
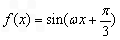 (x∈R,
(x∈R, )的图象如图,P是图象的最高点,Q是图象的最低点.且
)的图象如图,P是图象的最高点,Q是图象的最低点.且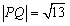 .
.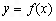 的解析式;
的解析式;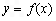 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数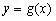 的图象,当
的图象,当 时,求函数
时,求函数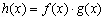 的最大值.
的最大值.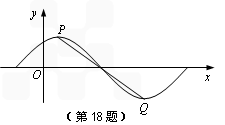
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一上学期期中数学试卷(解析版) 题型:解答题
(本题满分16分)
已知函数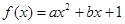 (
(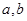 ∈R且
∈R且 ),
),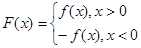 .
.
(Ⅰ)若 ,且函数
,且函数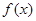 的值域为[0, +
的值域为[0, +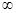 ),求
),求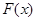 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时, 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设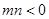 ,
,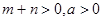 , 且
, 且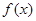 是偶函数,判断
是偶函数,判断 是否大于零?
是否大于零?
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第二次学情调研数学卷 题型:解答题
(本题满分16分)
已知函数 (
(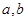 ∈R且
∈R且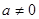 ),
),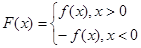 .
.
(Ⅰ)若 ,且函数
,且函数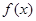 的值域为[0, +
的值域为[0, +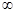 ),求
),求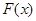 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时,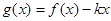 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设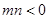 ,
,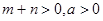 , 且
, 且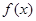 是偶函数,判断
是偶函数,判断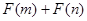 能否大于零?
能否大于零?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com