
分析 (1)求函数的导数,结合函数的极大值建立方程关系进行求解即可.
(2)根据函数极值的定义进行求解即可.
解答 解:(1)函数的导数f′(x)=3ax2+2bx,
∵当x=1时,函数有极大值3
∴$\left\{\begin{array}{l}{f(1)=3}\\{f′(1)=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a+b=3}\\{3a+2b=0}\end{array}\right.$.得$\left\{\begin{array}{l}{a=-6}\\{b=9}\end{array}\right.$,
经检验x=1是函数的极大值,
故a=-6,b=9.
(2)当a=-6,b=9时,f(x)=-6x3+9x2,
f′(x)=-18x2+18x,
由f′(x)>0得0<x<1,
由f′(x)<0得x>1或x<0,
即当x=1时函数取得极大值3,
当x=0时,函数取得极小值f(0)=0.
点评 本题主要考查函数极值的求解和应用,根据函数极值和函数导数之间的关系,建立方程关系是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
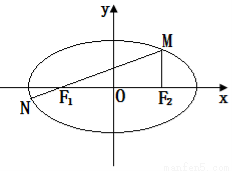
设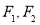 分别是椭圆
分别是椭圆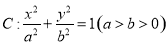 的左右焦点,
的左右焦点,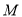 是
是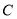 上一点,且
上一点,且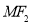 与
与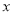 轴垂直,直线
轴垂直,直线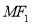 与
与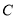 的另一个交点为
的另一个交点为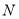 .
.
(1)若直线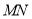 的斜率为
的斜率为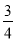 ,求
,求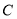 的离心率;
的离心率;
(2)若直线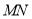 在
在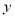 轴上的截距为2,且
轴上的截距为2,且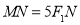 ,求椭圆
,求椭圆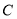 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
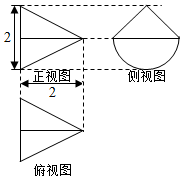 一个几何体的三视图如图所示,正视图与俯视图为全等的等腰三角形,侧视图由半圆和等腰直角三角形组成,则该几何体的体积为$\frac{π+2}{3}$.
一个几何体的三视图如图所示,正视图与俯视图为全等的等腰三角形,侧视图由半圆和等腰直角三角形组成,则该几何体的体积为$\frac{π+2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
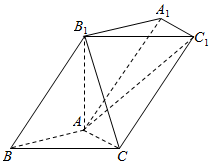 如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.
如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com