
����Ŀ��ÿ��5��17��Ϊ���ʵ����գ�ij�е��Ź�˾ÿ���ڵ����յ������Ӧ���ײ͵Ŀͻ������Żݣ��Żݷ������£�ѡ���ײ�һ�Ŀͻ��ɻ���Ż�200Ԫ��ѡ���ײͶ��Ŀͻ��ɻ���Ż�500Ԫ��ѡ���ײ����Ŀͻ��ɻ���Ż�300Ԫ������������ͳ�ƽ����������յ��������ͳ��ͼ���ֽ�Ƶ����Ϊ���ʣ�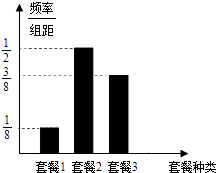
��1����ij����ѡ��ͬһ�ײ͵ĸ��ʣ�
��2�������������X��ʾij���������Żݽ����ܺͣ���X�ķֲ��к���ѧ������
���𰸡�
��1���⣺������ɵ�ij����ѡ��ͬһ�ײ͵ĸ���Ϊ��
![]() ��
��
��2��������֪ij���˿ɻ���Żݽ��X�Ŀ���ȡֵΪ400��500��600��700��800��1000. ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
���Ͽɵ�X�ķֲ���Ϊ��
X | 400 | 500 | 600 | 700 | 800 | 1000 |
P |
|
|
|
|
|
|
X����ѧ���� 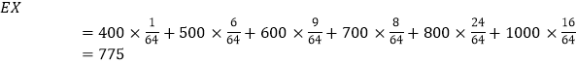 ��
��
����������1�����ùŵ���͵ĸ��ʹ�ʽ�������������ѡ��ͬһ�ײ͵ĸ��ʣ���2����֪X�Ŀ���ȡֵΪ400,500,600,700,800,1000�������Ӧ�ĸ��ʣ��г��ֲ��У����ݹ�ʽ���������


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ�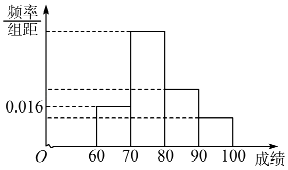
������˰༶������
�����涨Ԥ���ɼ�������90�ֵ�ѡ�ֲμӾ�������֪������λѡ���Ѿ�ȡ�þ����ʸμӾ�����ѡ�ְ���ǩ��ʽ��������˳��
��i���ײ����ڵ�һλ�Ҳ��������һλ�ĸ��ʣ�
��ii���Ǽ��Ҷ�������ǰ��λ������ΪX����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA=PB��PA��PB��AB��BC����ƽ��PAB��ƽ��ABCD����AB=2��BC=1�� ![]() ��
��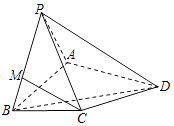
��1����֤��PA��ƽ��PBC��
��2������M����PB�ϣ���PM��MB=3����֤CM��ƽ��PAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0��1��2��3��4�����������ѡ������ͬ�������һ����λ������YΪ����ɵ���λ����λ����֮�ͣ�
��1����Y�������ĸ��ʣ�
��2����Y�ĸ��ʷֲ�����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ������˽�����ë����ϰ�����������˱�������һ�˵����У�ÿ�ֱ�������ʱ������һ�����¾ֵ����У�����ÿ�ֱ����У���ʤ�ҵĸ���Ϊ ![]() ����ʤ������ʤ���ĸ��ʶ���
����ʤ������ʤ���ĸ��ʶ��� ![]() �����ֱ����Ľ�����������һ�ּ����У�
�����ֱ����Ľ�����������һ�ּ����У�
��1�����3�ּ����еĸ��ʣ�
��2����ǰ4�����ҵ����еĴ���ΪX����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��������x0��[1��+�ޣ���ʹ�ã�log23�� ![]() ��1����������˵����ȷ���ǣ�������
��1����������˵����ȷ���ǣ�������
A.p�Ǽ����⣻�Vp������x��[1��+�ޣ������У�log23��x��1��
B.p�������⣻�Vp��������x0��[1��+�ޣ���ʹ�ã�log23�� ![]() ��1��
��1��
C.p�������⣻�Vp������x��[1��+�ޣ������У�log23��x��1��
D.p�Ǽ����⣻�Vp������x�ʣ����ޣ�1�������У�log23��x��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�ƽ��PAC�͵���ABCD��BC=CD= ![]() AC=2����ACB=��ACD=
AC=2����ACB=��ACD= ![]() ��
��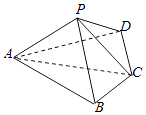
��1��֤����AP��BD��
��2����AP= ![]() ��AP��BC���ɽǵ�����ֵΪ
��AP��BC���ɽǵ�����ֵΪ ![]() ��������A��BP��C������ֵ��
��������A��BP��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�M����AD���е㣬O�ǵ�A�ڵ���BCD�ڵ���Ӱ��������ֱ��BM��AO���ɽǵ�����ֵΪ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ�M��AD��һ�㣮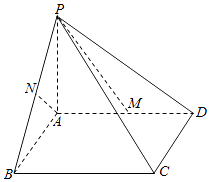
��1����֤��AB��PM��
��2����N��PB���е㣬��AN��ƽ��PCM���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com