练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    本小题满分14分

    正方形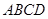的边长为1，分别取边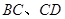的中点，连结，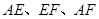   

    以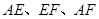为折痕，折叠这个正方形，使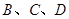点重合于一点，得到一   

    个四面体，如下图所示。

     

     

     

     

     


       

    （1）求证：；

    （2）求证：平面。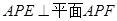

     

    【答案】

    证明：（1）由是正方形，所以在原图中

         折叠后有…………2分

         所以

          所以 …………7分

    （2）.由原图可知，

                 

                

          所以…………10分

         又，∴…………14分

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2011•广东模拟）（本小题满分14分 已知函数f(x)=
    		3
    sin2x+2sin(
    π
    4
    +x)cos(
    π
    4
    +x)    ．
    （I）化简f（x）的表达式，并求f（x）的最小正周期；
    （II）当x∈[0，
    π
    2
    ]  时，求函数f(x)    的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4，将4个这样的玩具同时抛掷于桌面上。

       （1）求与桌面接触的4个面上的4个数的乘积不能被4整除的概率；

       （2）设为与桌面接触的4个面上数字中偶数的个数， 求的分歧布列及期望E。

    查看答案和解析>>

    科目：高中数学 来源：2014届福建省高二上学期期中考试文科数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    已知二次函数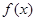满足以下两个条件：

    ①不等式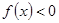的解集是（-2，0）   ②函数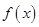在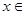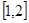上的最小值是3 

    （Ⅰ）求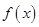的解析式；

     （Ⅱ）若点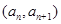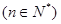在函数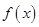的图象上，且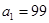

    （ⅰ）求证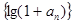：数列为等比数列

    （ⅱ）令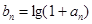，是否存在正实数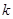，使不等式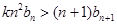对于一切的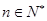恒成立？若存在，指出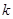的取值范围；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省宁波市鄞州区高三5月高考适应性理科数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    已知正项数列的首项，前项和满足．

    （Ⅰ）求数列的通项公式；

    （Ⅱ）若数列的前项和为，求证：．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年陕西省西安市高三下学期第一次模拟考试理科数学 题型：解答题

    （本小题满分14分）

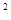    已知函数f(x)=x－ax + (a－1)，．

    （I）讨论函数的单调性；

    （II）若，数列满足．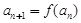

    （1）   若首项，证明数列为递增数列；

    （2）   若首项为正整数，数列递增，求首项的最小值．

     

     

    查看答案和解析>>

    同步练习册答案