
【题目】已知函数![]()
![]() .
.
(1)讨论函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若曲线![]() 仅在两个不同的点
仅在两个不同的点![]() ,
,![]() 处的切线都经过点
处的切线都经过点![]() ,其中
,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)先对函数求导,再分类分析讨论求解;(2)先依据导数的几何意义建立方程组,再抽象概括出方程有解,以此为前提构造函数,最后借助导数使得问题获解。
试题解析:
(1)证明:∵![]() ,∴
,∴![]() ,
,
∴![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,在区间
,在区间![]() 上,
上,![]() ,∴
,∴![]() 在区间
在区间![]() 上递减.
上递减.
当![]() 时,
时,![]() ,在区间
,在区间![]() 上,
上,![]() ,∴
,∴![]() 在区间
在区间![]() 上递增.
上递增.
当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,∴
,∴![]() 在区间
在区间![]() 上递增;
上递增;
在区间![]() 上,
上,![]() ,∴
,∴![]() 在区间
在区间![]() 上递减.
上递减.
(2)曲线![]() 在
在![]() 两点处的切线的方程分别为
两点处的切线的方程分别为
![]() ,
,
![]() .
.
设![]() ,将
,将![]() 代入两条切线方程,得
代入两条切线方程,得
![]() ,
,
![]() .
.
由题可得方程![]() 即
即![]() 有且仅有不相等的两个实根.
有且仅有不相等的两个实根.
设![]() ,
,
![]() .
.
①当![]() 时,
时,![]() ,∴
,∴![]() 单调递增,显然不成立.
单调递增,显然不成立.
②当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() .
.
∴![]() 的极值分别为
的极值分别为![]() ,
,![]() .
.
要使得关于![]() 的方程
的方程![]() 有且仅有两个不相等的实根,
有且仅有两个不相等的实根,
则![]() 或
或![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,(1),或
,(1),或![]() .(2)
.(2)
解(1),得![]() ,解(2),得
,解(2),得![]() 或
或![]() .
.
∵![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为2.10元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元.已知甲、乙两用户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)如甲、乙两户该月共交水费40.8元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
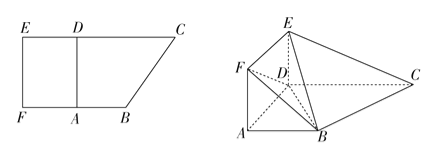
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对任意实数
,对任意实数![]() ,都有
,都有![]() .
.
(1)若![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 为常数,函数
为常数,函数![]() 是奇函数,
是奇函数,
①验证函数![]() 满足题中的条件;
满足题中的条件;
②若函数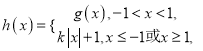 求函数
求函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且资金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但资金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家医药研究所,从中草药中提取并合成了甲、乙两种抗“![]() 病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为
病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为![]() .现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.
.现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.
(1)求一个试用组为“甲类组”的概率;
(2)观察3个试用组,用![]() 表示这3个试用组中“甲类组”的个数,求
表示这3个试用组中“甲类组”的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com