
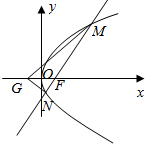
 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2分析 (1)根据AF=2,求得m=2-$\frac{p}{2}$.再把点A(m,2)代入抛物线C的方程,求得p的值,可得抛物线C的方程.
(2)设MN的方程为y-0=k(x-1),代入抛物线C:y2=4x,利用韦达定理.要证∠MGF=∠NGF,只要证GM、GN的斜率相反即可.再根据GM、GN斜率之和为$\frac{{y}_{1}}{{x}_{1}+1}$+$\frac{{y}_{2}}{{x}_{2}+1}$,利用韦达定理求得它为零,从而证得结论.
解答 解:(1)由题意可得F($\frac{p}{2}$,0),AF=2=m-(-$\frac{p}{2}$)=m+$\frac{p}{2}$,即m=2-$\frac{p}{2}$.
再把点A(m,2)代入抛物线C:y2=2px,可得4=2p(2-$\frac{p}{2}$),求得p=2,
故抛物线C的方程:y2=4x,故焦点F(1,0).
(2)设MN的方程为y-0=k(x-1),即 y=kx-k,代入抛物线C:y2=4x 可得k2•x2-(2k2+4)x+k2=0,
∴x1+x2=$\frac{{2k}^{2}+4}{{k}^{2}}$=2+$\frac{4}{{k}^{2}}$,x1•x2=1.
要证∠MGF=∠NGF,只要证GM、GN的斜率相反即可,即GM、GN斜率之和等于零.
再根据GM、GN斜率之和为 $\frac{{y}_{1}}{{x}_{1}+1}$+$\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{{kx}_{1}-k}{{x}_{1}+1}$+$\frac{{kx}_{2}-k}{{x}_{2}+1}$=$\frac{k{(x}_{1}-1){(x}_{2}+1)+k{(x}_{2}-1){(x}_{1}+1)}{{(x}_{1}+1){(x}_{2}+1)}$=$\frac{2k{(x}_{1}{•x}_{2}-1)}{{(x}_{1}+1){(x}_{2}+1)}$=0,
故∠MGF=∠NGF成立.
点评 本题主要考查抛物线的标准方程,直线和圆锥曲线的位置关系,韦达定理,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | [-2,+∞) | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
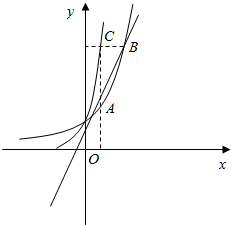 如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{5}{4}$ | B. | ±$\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | -$\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com