
【题目】【2015高考广东,文19】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() ,且当
,且当![]()
时,![]() .
.
(1)求![]() 的值;
的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列![]() 的通项公式.
的通项公式.
科目:高中数学 来源: 题型:
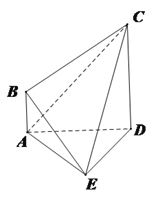
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(2)若函数![]() 在定义域内不单调,求
在定义域内不单调,求![]() 的取值范围;
的取值范围;
(3)是否存在正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 满足关系
满足关系![]() (其中
(其中![]() 是常数).
是常数).
(![]() )如果
)如果![]() ,
, ![]() ,求函数
,求函数![]() 的值域;
的值域;
(![]() )如果
)如果![]() ,
, ![]() ,且对任意
,且对任意![]() ,存在
,存在![]() ,
, ![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(![]() )如果
)如果![]() ,求函数
,求函数![]() 的最小正周期(只需写出结论).
的最小正周期(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=![]() ﹣p
﹣p
④回归直线一定过样本点的中心(![]() ).
).
其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
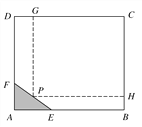
【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com