
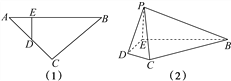
【题目】如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).
(1)求证:PB⊥DE;
(2)若PE⊥BE,PE=1,求点B到平面PEC的距离.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)根据线面垂直的判定定理和性质定理进行证明,(2)由(1)知PE⊥平面BEDC,在△EDC中,由余弦定理得EC=![]() ,S△PEC=
,S△PEC=![]() ×PE×EC=
×PE×EC=![]() .利用等体积法VP-BEC=VB-PEC进行求解即可得点B到平面PEC的距离.
.利用等体积法VP-BEC=VB-PEC进行求解即可得点B到平面PEC的距离.
试题解析:
(1)∵DE⊥AB,∴DE⊥PE,DE⊥EB.
又∵PE∩BE=E,∴DE⊥平面PEB.∵PB平面PEB,∴PB⊥DE.
(2)由(1)知DE⊥PE,且PE⊥BE,DE∩BE=E,∴PE⊥平面BEDC.
连接EC,∵PE=1,
∴DE=PE=1,AD=DC=![]() .
.
在△EDC中,∠EDC=135°,由余弦定理得
EC2=DE2+DC2-2DE×DC×cos∠EDC=1+2-2![]() ×(-
×(-![]() )=5,
)=5,
∴EC=![]() ,∴S△PEC=
,∴S△PEC=![]() ×PE×EC=
×PE×EC=![]() .
.
设点B到平面PEC的距离为h,则由VP-BEC=VB-PEC得![]() S△PEC·h=
S△PEC·h=![]() S△BEC·PE,
S△BEC·PE,
∴![]() h=
h=![]() ×3×2×1,∴h=
×3×2×1,∴h=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米,圆心角为
米,圆心角为![]() (弧度)的扇形观景水池,其中
(弧度)的扇形观景水池,其中![]() ,
, ![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边(即:
的圆心,同时紧贴水池周边(即: ![]() 和
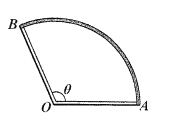
和![]() 所对的圆弧)建设一圈理想的无宽度步道.要求总预算费用不超过24万元,水池造价为每平方米400元,步道造价为每米1000元.
所对的圆弧)建设一圈理想的无宽度步道.要求总预算费用不超过24万元,水池造价为每平方米400元,步道造价为每米1000元.
(1)若总费用恰好为24万元,则当![]() 和
和![]() 分别为多少时,可使得水池面积最大,并求出最大面积;
分别为多少时,可使得水池面积最大,并求出最大面积;
(2)若要求步道长为105米,则可设计出的水池最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() (
(![]() ,
, ![]() 为常数).
为常数).
(1)判断曲线![]() 的形状;
的形状;
(2)设曲线![]() 分别与
分别与![]() 轴,
轴, ![]() 轴交于点
轴交于点![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原点
不同于原点![]() ),试判断
),试判断![]() 的面积
的面积![]() 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线![]() :
: ![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-f′(0)ex+2x,点P为曲线y=f(x)在点(0,f(0))处的切线l上的一点,点Q在曲线y=ex上,则|PQ|的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)当a<0时,讨论f(x)的单调性;
(2)若对任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位:千克)全部介于![]() 至
至![]() 之间,将数据分成以下
之间,将数据分成以下![]() 组,第一组
组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组,第五组
,第四组,第五组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第![]() 、
、![]() 、
、![]() 组中随机抽取
组中随机抽取![]() 名学生做初检.
名学生做初检.
(Ⅰ)求每组抽取的学生人数.
(Ⅱ)若从![]() 名学生中再次随机抽取
名学生中再次随机抽取![]() 名学生进行复检,求这
名学生进行复检,求这![]() 名学生不在同一组的概率.
名学生不在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动,规则是每邀请一位好友在该平台注册,并购买至少1万元的12月定期,邀请人可获得现金及红包奖励,现金奖励为被邀请人理财金额的![]() ,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
理财金额 |
|
|
|
乙理财相应金额的概率 |
|
|
|
丙理财相应金额的概率 |
|
|
|
(1)求乙、丙理财金额之和不少于5万元的概率;
(2)若甲获得奖励为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com