
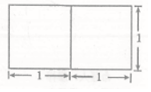
 一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )
一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )| A. | $\frac{19}{6}$ | B. | $\frac{38}{3}$ | C. | $\frac{57}{8}$ | D. | $\frac{19}{3}$ |
分析 由已知中底面是正三角形的三棱柱的正视图,求出三棱柱的底面边长和高,从而求出它外接球的半径,再求球内接正方体的棱长,即可求出其表面积.
解答 解:由已知中的三棱柱正视图可得:
三棱柱的底面边长为2,高为1
则三棱柱的底面外接圆半径为
r=$\frac{2\sqrt{3}}{3}$,
球心到底面的距离为
d=$\frac{1}{2}$;
则球的半径为
R=$\sqrt{{r}^{2}{+d}^{2}}$=$\sqrt{\frac{19}{12}}$;
∴该球的内接正方体对角线长是
2R=2$\sqrt{\frac{19}{12}}$=$\sqrt{3}$a,
∴a=2$\sqrt{\frac{19}{36}}$=$\frac{\sqrt{19}}{3}$;
∴内接正方体的表面积为:
S=6a2=6×$\frac{19}{9}$=$\frac{38}{3}$.
故选:D.
点评 本题考查了球与三棱柱、正方体的关系与应用问题,根据条件确定三棱柱的底面边长和高,根据棱柱的底面外接圆半径,球心距,球半径求出球半径是解题关键.


科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
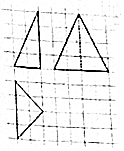
| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 回归分析 | B. | 独立性检验分析 | C. | 残差分析 | D. | 散点图分析 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com