
【题目】淮北市第一次模拟考试理科共考语文、数学、英语、物理、化学、生物六科,安排在某两日的四个半天考完,每个半天考一科或两科.若语文、数学、物理三科中任何两科不能排在同一个半天,则此次考试不同安排方案的种数有( )(同一半天如果有两科考试不计顺序)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.
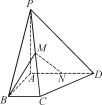
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() /次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比率 |
|
|
|
|
|
该公司注册的会员中没有消费超过![]() 次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
消费次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元,根据所给数据,解答下列问题:
元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折,如![]() ,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国历法中将一年分为春、夏、秋、冬四个季节,每个季节有六个节气,如夏季包含立夏、小满、芒种、夏至、小暑以及大暑.某美术学院甲、乙、丙、丁四位同学接到绘制二十四节气的彩绘任务,现四位同学抽签确定各自完成哪个季节中的六幅彩绘,在制签及抽签公平的前提下,甲没有抽到绘制春季六幅彩绘任务且乙没有抽到绘制夏季六幅彩绘任务的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
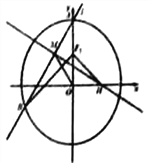
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点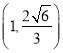 .
.
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点T为圆![]() 上一动点,过点T分别作x轴,y轴的垂线,垂足分别为A,B,连接BA延长至点P,使得
上一动点,过点T分别作x轴,y轴的垂线,垂足分别为A,B,连接BA延长至点P,使得![]() ,点P的轨迹记为曲线C.
,点P的轨迹记为曲线C.
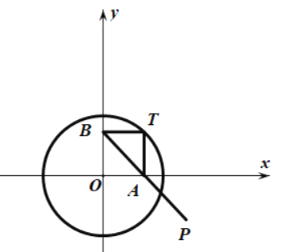
(1)求曲线C的方程;
(2)若点A,B分别位于x轴与y轴的正半轴上,直线AB与曲线C相交于M,N两点,试问在曲线C上是否存在点Q,使得四边形OMQN为平行四边形,若存在,求出直线l方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com