分析:(1)过B
1点作B
1O⊥BA,说明∠B
1BA是侧面BB
1与底面ABC倾斜角,在三角形Rt△B
1OB中,计算BO=
AB,从而证明点B
1在平面ABC上的射影O为AB的中点;
(2)连接AB
1过点O作OM⊥AB
1,连线CM,OC,说明∠OMC是二面角C-AB
1-B的平面角,在Rt△OCM中,去求二面角C-AB
1-B的大小;
(3)过点O作ON⊥CM,推出ON是O点到平面AB
1C的距离,连接BC
1与B
1C相交于点H,则H是BC
1的中点,B到平面AB
1C的距离
是O到平面AB
1C距离的2倍,即可求点C
1到平面CB
1A的距离.
解答: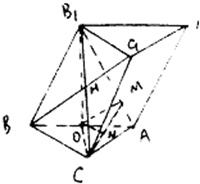
解:(1)证明:过B
1点作B
1O⊥BA.∵侧面ABB
1A
1⊥底面ABC
∴A
1O⊥面ABC∴∠B
1BA是侧面BB
1与底面ABC倾斜角
∴∠B
1BO=
在Rt△B
1OB中,BB
1=2,∴BO=
BB
1=1
又∵BB
1=AB,∴BO=
AB∴O是AB的中点.
即点B
1在平面ABC上的射影O为AB的中点(4分)
(2)连接AB
1过点O作OM⊥AB
1,连线CM,OC,
∵OC⊥AB,平面ABC⊥平面AA
1BB
1∴OC⊥平面AABB.
∴OM是斜线CM在平面AA
1B
1B的射影∵OM⊥AB
1∴AB
1⊥CM∴∠OMC是二面角C-AB
1-B的平面角
在Rt△OCM中,OC=
,OM=
,∴
tan∠OMC==2∴∠OMC=cosC+sin2
∴二面角C-AB
1-B的大小为arctan2.(8分)
(3)过点O作ON⊥CM,∵AB
1⊥平面OCM,∴AB
1⊥ON
∴ON⊥平面AB
1C.∴ON是O点到平面AB
1C的距离
在Rt△OMC中,
OC=,OM=.∴
CM==∴
ON===连接BC
1与B
1C相交于点H,则H是BC
1的中点
∴B与C
1到平面ACB
1的相等.
又∵O是AB的中点∴B到平面AB
1C的距离
是O到平面AB
1C距离的2倍
是G到平面AB
1C距离为
.(12分)
点评:本题考查点、线、面间的距离计算,二面角及其度量,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

 已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为
已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为 解:(1)证明:过B1点作B1O⊥BA.∵侧面ABB1A1⊥底面ABC
解:(1)证明:过B1点作B1O⊥BA.∵侧面ABB1A1⊥底面ABC

 名校课堂系列答案
名校课堂系列答案 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°. 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点. 如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl
已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl