
【题目】(本题满分16分)第1小题5分,第2小题5分,第3小题6分.
已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1) 若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2) 当![]() 时,设
时,设![]() 的反函数为
的反函数为![]() ,且函数
,且函数![]() 的图像与
的图像与![]() 的图像关于
的图像关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3) 对于问题(1)(2)中的![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
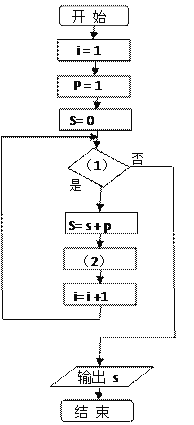
【题目】给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.将右边给出的程序框图补充完整,
(1)___________________ (2)_______________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段AB中点为C,当线段AB的两个端点A和B分别在x轴和y轴上运动时,C点的轨迹为曲线C1;
(1)求曲线C1的方程;
(2)直线 ![]() ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() :
:![]() (
(![]() 为参数),经过伸缩变换
为参数),经过伸缩变换![]() 后得到曲线
后得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)若点![]() 的曲线
的曲线![]() 上运动,试求出
上运动,试求出![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲制作容积为16米3 , 高为1米的无盖长方体容器,已知该容器的底面造价是每平方米1000元,侧面造价是每平方米500元,记该容器底面一边的长为x米,容器的总造价为y元.
(1)试用x表示y;
(2)求y的最小值及此时该容器的底面边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
A.6
B.8
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B的坐标分别是 ![]() ,点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|. (Ⅰ)求△ABC的顶点C的轨迹E的方程;
,点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|. (Ⅰ)求△ABC的顶点C的轨迹E的方程;
(Ⅱ)直线l:y=kx+m与轨迹E相交于P,Q两点,若在轨迹E上存在点R,使四边形OPRQ为平行四边形(其中O为坐标原点),求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com