
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AD∥BC,AD=2BC=2,PC=2,△ABC是以AC为斜边的等腰直角三角形,E是PD的中点.
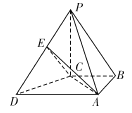
(1)求证:平面EAC⊥平面PCD;
(2)求直线PA与平面EAC所成角的正弦值.
【答案】(1)见解析.
(2) ![]() .
.
【解析】分析:(1)推导出![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
;
(2)作![]() ,则
,则![]() 平面
平面![]() ,从而
,从而![]() 与平面
与平面![]() 所成角
所成角![]() ,由此能求出
,由此能求出![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
详解:(1)证明:∵PC⊥底面ABCD,AC底面ABCD,
∴PC⊥AC1分
由题意可知,AD∥BC,且AD=2BC=2,
△ABC是等腰直角三角形.
∴AC=![]() BC=
BC=![]() ,CD=
,CD=![]() 2分
2分
∴CD2+AC2=AD2,即AC⊥CD,3分
又∵PC∩CD=C4分
∴AC⊥平面PCD5分
∵AC平面EAC
∴平面EAC⊥平面PCD6分
(2)由(1)得平面EAC⊥平面PCD,
平面EAC∩平面PCD=EC,
作PH⊥EC,∴PH⊥平面EAC8分
所以PA与平面EAC所成角为∠PAH9分
在Rt△PAC中,PA=![]() ,
,
在Rt△PHC中,sin∠PCE=![]() ,PH=PCsin∠PCE=
,PH=PCsin∠PCE=![]() 10分
10分
sin∠PAH=![]() =
=![]() =
=![]() ,所以直线PA与平面EAC所成角的正弦值为
,所以直线PA与平面EAC所成角的正弦值为![]() 12分
12分



科目:高中数学 来源: 题型:
【题目】某服装超市举办了一次有奖促销活动,顾客消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性抽出3个小球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球则打6折,若摸到1个红球,则打7折;若没有摸到红球,则不打折;
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回的摸取,连续3次,每摸到1个红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,则该顾客选择哪种抽奖方案更合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α过正方体ABCD﹣A1B1C1D1的面对角线 ![]() ,且平面α⊥平面C1BD,平面α∩平面ADD1A1=AS,则∠A1AS的正切值为( )
,且平面α⊥平面C1BD,平面α∩平面ADD1A1=AS,则∠A1AS的正切值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流传多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小千和大年两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小千和大年比赛至第四局小千胜出的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,倾斜角为
中,倾斜角为 ![]() 的直线
的直线 ![]() 过点
过点 ![]() ,以原点
,以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出直线 ![]() 的参数方程(
的参数方程( ![]() 为常数)和曲线
为常数)和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 与
与 ![]() 交于
交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() ,求倾斜角
,求倾斜角 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班![]() 人的成绩记为
人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
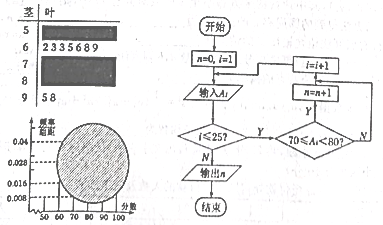
注:图中![]() 表示“是”,
表示“是”,![]() 表示“否”
表示“否”
(1)求茎叶图中破损处分数在![]() ,
,![]() ,
,![]() 各区间段的频数;
各区间段的频数;
(2)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com