
【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
(1)画散点图;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值:![]() )
)
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣0.8x%)万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.4x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创遣的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间在两天内,每天生产10件某产品,其中第一天第二天分别生产了1件2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(1)求两天全部通过检查的概率;
(2)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元900元.那么该车间在这两天内得到奖金的数学期望是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
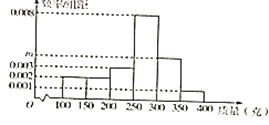
【题目】炎炎夏季,水蜜桃成为备受大家欢迎的一种水果,某果园的水蜜桃质量分布如图所示.
(Ⅰ)求m的值;
(Ⅱ)以频率估计概率,若从该果园中随机采摘5个水蜜桃,记质量在300克以上(含300克)的个数为X,求X的分布列及数学期望;
(Ⅲ)经市场调查,该种水蜜桃在过去50天的销售量(单位:千克)和价格(单位:元/千克)均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣3t+300(1≤t≤50,t∈N),前30天价格为g(t)=![]() +20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
+20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com