
| a |
| b |
| a |
| 2 |
| b |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| c |
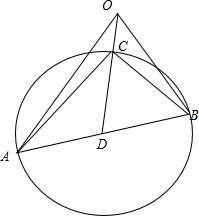
| OA |
| a |
| OB |
| b |
| OC |
| c |
| π |
| 4 |
| CA |
| CB |
| OC |
| c |
| a |
 解:由已知条件知,向量
解:由已知条件知,向量| a |
| b |
| π |
| 4 |
| a |
| c |
| b |
| c |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| c |
| CA |
| b |
| c |
| CB |
| CA |
| CB |
| OC |
| c |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| 5 |
| ||
sin
|
| 1 |
| sin∠OAB |
| ||
| 10 |
3
| ||
| 10 |
| 5 |
| 4 |
| 2 |
| ||
| 2 |
3
| ||
| 10 |
| 13 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 2 |
| c |
| ||||
| 2 |
| ||||
| 2 |
| π |
| 2 |


科目:高中数学 来源: 题型:
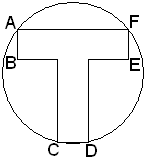 某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:①“T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“T型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com