
【题目】某工厂为生产一种精密管件研发了一台生产该精密管件的车床,该精密管件有内外两个口径,监管部门规定“口径误差”的计算方式为:管件内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() 则“口径误差”为
则“口径误差”为![]() 只要“口径误差”不超过
只要“口径误差”不超过![]() 就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
(Ⅰ)以上述样本的频率作为概率,在昼夜两个批次中分别抽取2件产品,求其中恰有1件不合格产品的概率;
(Ⅱ)若每批次各生产1000件,已知每件产品的成本为5元,每件合格品的利润为10元;若对产品检验,则每件产品的检验费用为2.5元;若有不合格品进入用户手中,则工厂要对用户赔偿,这时生产的每件不合格品工厂要损失25元.以上述样本的频率作为概率,以总利润的期望值为决策依据,分析是否要对每个批次的所有产品作检测?
【答案】(Ⅰ)![]() ;(Ⅱ)昼批次不做检測为好;夜批次做检测为优.
;(Ⅱ)昼批次不做检測为好;夜批次做检测为优.
【解析】
(Ⅰ)先分别求出昼批次和夜批次合格品的概率,再由独立事件同时发生的概率公式,即可求解;
(Ⅱ)分别求出昼批次和夜批次不做检测的利润期望值和都做检测的利润期望值,加以对比,即可得出结论.
(Ⅰ)以样本的频率作为概率,在昼批次中随机抽取1件为合格品的概率是![]() ,
,
在夜批次中随机抽取1件为合格品的概率是![]() ,
,
故两个批次中分别抽取2件产品,其中恰有1件不合格产品的概率为![]() .
.
(Ⅱ)①若对所有产品不做检测,
设![]() 为昼批次中随机抽取1件的利润,
为昼批次中随机抽取1件的利润,![]() 的可能取值为10,
的可能取值为10,![]() ,
,
所以![]() 的分布列为
的分布列为
| 10 |
|
| 0.9 | 0.1 |
所以![]() ,
,
故在不对所有产品做检测的情况下,
1000件产品的利润的期望值为![]() ,
,
设![]() 为夜批次中随机抽取1件的利润,
为夜批次中随机抽取1件的利润,![]() 的可能取值为10,
的可能取值为10,![]() ,
,
所以![]() 的分布列为
的分布列为
| 10 |
|
| 0.75 | 0.25 |
所以![]() ,
,
故在不对所有产品做检测的情况下,
1000件产品的利润的期望值为![]() ,
,
②若对所有产品做检测,
昼批次1000件产品的合格品的期望为900件,不合格品的期望为100件,
所以利润为![]() ,
,
夜批次1000件产品的合格品的期望为750件,不合格品的期望为250件,
所以利润为![]() ,
,
综上,昼批次不做检测的利润期望6500大于做检測的利润期望6000,
故昼批次不做检測为好;
夜批次不做检测的利润期望1250小于做检测的利润期望3750,
故夜批次做检测为优.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】新高考取消文理科,实行“3+3”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年),并把调查结果制成如表:

(1)请根据上表完成下面2×2列联表,并判断是否有95%的把握认为对新高考的了解与年龄(中青年、中老年)有关?
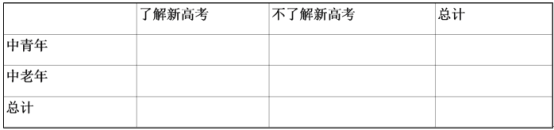
附:K2![]() .
.

(2)现采用分层抽样的方法从中老年人中抽取8人,再从这8人中随机抽取2人进行深入调查,求事件A:“恰有一人年龄在[45,55)”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒(![]() 肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为
肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为![]() ,
,![]() 两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下
两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下![]() 的列联表.
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
(1)分别估计社区居民对![]() 组、
组、![]() 组两个排查组的工作态度满意的概率;
组两个排查组的工作态度满意的概率;
(2)根据列联表的数据,能否有![]() 的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: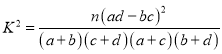
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(0,2),B(0,﹣2),动点P(x,y)满足PA,PB的斜率之积为![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m,C的右焦点为F,直线l与C交于M,N两点,若F是△AMN的垂心,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过![]() 的部分按照平价收费,超过
的部分按照平价收费,超过![]() 的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组
的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组![]() 制作了频率分布直方图,
制作了频率分布直方图,
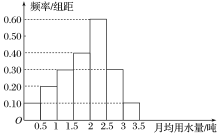
(1)从频率分布直方图中估计该40位居民月均用水量的众数,中位数;
(2)在该样本中月均用水量少于1吨的居民中随机抽取两人,其中两人月均用水量都不低于0.5吨的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com