
【题目】已知函数![]() 为二次函数,不等式
为二次函数,不等式![]() 的解集是
的解集是![]() ,且
,且![]() 在区间
在区间![]() 上的最大值为12.
上的最大值为12.
(1)求![]() 的解析式;
的解析式;
(2)设函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的表达式及
的表达式及![]() 的最小值.
的最小值.
【答案】(1)![]() .(2)
.(2)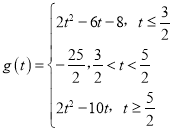 .最小值
.最小值![]()
【解析】
(1)根据![]() 是二次函数,且
是二次函数,且![]() 的解集是
的解集是![]() 可设出
可设出![]() 的零点式,再根据在区间
的零点式,再根据在区间![]() 上的最大值在对称轴处取得为12即可算出对应的参数.
上的最大值在对称轴处取得为12即可算出对应的参数.
(2)由(1)求得![]() 后改写成顶点式,再根据对称轴与区间的位置关系,分情况进行讨论即可.
后改写成顶点式,再根据对称轴与区间的位置关系,分情况进行讨论即可.
(1)![]() 是二次函数,且
是二次函数,且![]() 的解集是
的解集是![]() ,
,
∴可设![]() ,
,
可得在区间![]() 在区间
在区间![]() 上函数是减函数,区间
上函数是减函数,区间![]() 上函数是增函数.
上函数是增函数.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,得
,得![]() .
.
因此,函数的表达式为![]() .
.
(2)由(1)得![]() ,函数图象的开口向上,对称轴为
,函数图象的开口向上,对称轴为![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
此时![]() 的最小值
的最小值![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
此时![]() 的最小值
的最小值![]() ;
;
③当![]() 时,函数
时,函数![]() 在对称轴处取得最小值,
在对称轴处取得最小值,
此时,![]() ,
,
综上所述,得![]() 的表达式为
的表达式为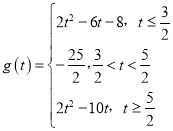 ,
,
当![]() ,
,![]() 取最小值
取最小值![]()


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为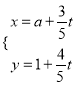 (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,
, ![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每天下雨的概率都为![]() .现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用
.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用![]() 表示下雨,从下列随机数表的第
表示下雨,从下列随机数表的第![]() 行第
行第![]() 列的
列的![]() 开始读取,直到读取了
开始读取,直到读取了![]() 组数据,
组数据,
18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10
55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24
据此估计,这三天中恰有两天下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() ,且
,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)设函数 ,记
,记![]()
![]() .探究是否存在正整数
.探究是否存在正整数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有满足条件的正整数
恒成立?若存在,求出所有满足条件的正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
. ![]() 为椭圆的右焦点,
为椭圆的右焦点, ![]() 为椭圆上关于原点对称的两点,连接
为椭圆上关于原点对称的两点,连接![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
⑴求椭圆的标准方程;
⑵若![]() ,求
,求![]() 的值;
的值;
⑶设直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ;
;
②若![]() (
(![]() 且
且![]() ),则
),则![]() 的取值范围是
的取值范围是![]() ;
;
③若函数![]() ,则对任意的
,则对任意的![]() ,都有
,都有![]() ;
;
④若![]() (
(![]() 且
且![]() ),在区间
),在区间![]() 上单调递减,则
上单调递减,则![]() .
.
其中所有正确命题的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医药公司针对某种疾病开发了一种新型药物,患者单次服用制定规格的该药物后,其体内的药物浓度![]() 随时间
随时间![]() 的变化情况(如图所示):当
的变化情况(如图所示):当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数);当
为常数);当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).服药
为常数).服药![]() 后,患者体内的药物浓度为
后,患者体内的药物浓度为![]() ,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
(1)首次服药后,药物有疗效的时间是多长?
(2)首次服药1小时后,可否立即再次服用同种规格的这种药物?
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
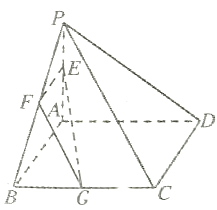
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,E、F、G分别是PA、PB、BC的中点
(1)证明:平面EFG∥平面PCD;
(2)若平面EFG截四棱锥P-ABCD所得截面的面积为![]() ,求四棱锥P-ABCD的体积
,求四棱锥P-ABCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为![]() ,
,![]() .这两条曲线在第一象限的交点为
.这两条曲线在第一象限的交点为![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为![]() 、
、![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com