
【题目】如图,在三棱锥![]() 中,
中,![]() 平面ABC,点D,E,F分别为PC,AB,AC的中点.
平面ABC,点D,E,F分别为PC,AB,AC的中点.
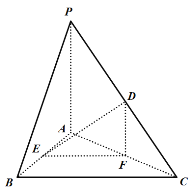
(Ⅰ)求证:![]() 平面DEF;
平面DEF;
(Ⅱ)求证:![]() .
.
阅读下面给出的解答过程及思路分析.
解答:(Ⅰ)证明:在![]() 中,因为E,F分别为AB,AC的中点,所以①.
中,因为E,F分别为AB,AC的中点,所以①.
因为![]() 平面DEF,
平面DEF,![]() 平面DEF,所以
平面DEF,所以![]() 平面DEF.
平面DEF.
(Ⅱ)证明:因为![]() 平面ABC,
平面ABC,![]() 平面ABC,所以②.
平面ABC,所以②.
因为D,F分别为PC,AC的中点,所以![]() .所以
.所以![]() .
.
思路第(Ⅰ)问是先证③,再证“线面平行”;
第(Ⅱ)问是先证④,再证⑤,最后证“线线垂直”.
以上证明过程及思路分析中,设置了①~⑤五个空格,如下的表格中为每个空格给出了三个选项,其中只有一个正确,请选出你认为正确的选项,并填写在答题卡的指定位置.
空格 | 选项 | ||
① | A. | B. | C. |
② | A. | B. | C. |
③ | A.线线垂直 | B.线面垂直 | C.线线平行 |
④ | A.线线垂直 | B.线面垂直 | C.线线平行 |
⑤ | A.线面平行 | B.线线平行 | C.线面垂直 |
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ,
,![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=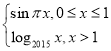 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A. (1,2015)B. (1,2016)
C. [2,2 016]D. (2,2016)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() .
.

(1)证明:![]() ;
;
(2)设![]() 是线段
是线段![]() 上的动点,是否存在这样的点
上的动点,是否存在这样的点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,如果存在,求出
,如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】土壤重金属污染已经成为快速工业化和经济高速增长地区的一个严重问题,污染土壤中的某些重金属易被农作物吸收,并转入食物链影响大众健康.A,B两种重金属作为潜在的致癌物质,应引起特别关注.某中学科技小组对由A,B两种重金属组成的1000克混合物进行研究,测得其体积为100立方厘米(不考虑物理及化学变化),已知重金属A的密度大于![]() ,小于
,小于![]() ,重金属B的密度为
,重金属B的密度为![]() .试计算此混合物中重金属A的克数的范围.
.试计算此混合物中重金属A的克数的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() 为直角三角形,求直线
为直角三角形,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大豆,古称菽,原产中国,在中国已有五千年栽培历史,皖北多平原地带,黄河故道土地肥沃,适宜种植大豆,2018年春,为响应中国大豆参与世界贸易的竞争,某市农科院积极研究,加大优良品种的培育工作,其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系,为此科研人员分别记录了5天中每天100粒大豆的发芽数,得如下数据表格:

科研人员确定研究方案是:从5组数据中选3组数据求线性回归方程,再用求得的回归方程对剩下的2组数据进行检验.
(Ⅰ)求剩下的2组数据恰是不相邻的2天数据的概率;
(Ⅱ)若选取的是4月5日、6日、7日三天数据,据此求![]() 关于
关于![]() 的线性同归方程
的线性同归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒,则认为得到的线性回归方程是可靠的,请检验(Ⅱ)中同归方程是否可靠?
注: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com