
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出当![]() 时直线
时直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且
,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且![]() 。
。
(1)抛物线C的标准方程;
(2)若在x轴上存在点M,过点M的直线l分别与抛物线C相交于P、Q两点,且![]() 为定值,求点M的坐标.
为定值,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,若动点
,若动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,请问在曲线
,请问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() (
(![]() 为坐标原点)为平行四边形?若存在,求出直线
为坐标原点)为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某中学高二年级共有8个班,现从高二年级选10名同学组成社区服务小组,其中高二(1)班选取3名同学,其它各班各选取1名同学.现从这10名同学中随机选取3名同学到社区老年中心参加“尊老爱老”活动(每位同学被选到的可能性相同).
(1)求选出的3名同学来自不同班级的概率;
(2)设![]() 为选出的同学来自高二(1)班的人数,求随机变量
为选出的同学来自高二(1)班的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)若M(m,n),求![]() 的最大值和最小值
的最大值和最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线![]() 与椭圆
与椭圆![]() 有且仅有一个交点
有且仅有一个交点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与
与![]() 轴交于
轴交于![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于两不同点
交于两不同点![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《国家中长期教育改革和发展规划2010-2020》指出,到2020年基本实现教育现代化,进入人力资源强国行列,并提出要实现更高水平的普及教育,基本普及学前教育、巩固提高九年义务教育、提高高等教育大众化水平,从国家层面确立了教育的重要地位.随着国家对教育的日益重视,教育经费投入也逐渐加大.下图是我国2010年到2016年国家财政性教育经费投入(单位:万亿元)的散点图,年份代码为![]() .
.

注:年份代码1-7分别对应年份2010-2016.
(1)由散点图可知国家财政性教育经费投入![]() 与年份代码
与年份代码![]() 具有相关关系,试建立国家财政性教育经费投入
具有相关关系,试建立国家财政性教育经费投入![]() 与年份代码
与年份代码![]() 的回归方程;
的回归方程;
(2)预测2020年我国国家财政性教育经费投入的值是否能超过![]() 万亿.
万亿.
附注:参考数据:![]() ,
,![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: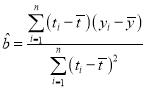 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com