
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
【答案】(1)![]() ; (2)1; (3)见解析.
; (2)1; (3)见解析.
【解析】
(1)设直线AB的方程,联立抛物线方程,运用韦达定理,可得p=4,即得抛物线方程;(2)推理证明![]() =
=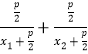 ,整理即可得到所求值;(3)设A(
,整理即可得到所求值;(3)设A(![]() ,y1),B(
,y1),B(![]() ,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
(1)过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线
的直线
为![]() ,代入抛物线方程,可得
,代入抛物线方程,可得![]() ,
,
可设![]() ,
,
即有![]() ,解得
,解得![]() ,
,
可得抛物线的方程为![]() ;
;
(2)由直线![]() 过抛物线的焦点
过抛物线的焦点![]() ,
,
由(1)可得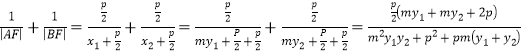 ,将
,将![]() 代入可得
代入可得![]() ;
;
(3)证明:设![]() ,
,![]() ,
,![]() ,
,
由![]() 三点共线可得
三点共线可得
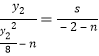 ,可得
,可得![]() ,①
,①
设![]() 交
交![]() 轴上的点为
轴上的点为![]() ,即有
,即有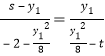 ,
,
代入①,结合![]() ,可得
,可得![]() ,
,
即有![]() ,
,
可得![]() .即有直线
.即有直线![]() 与
与![]() 轴交于一定点
轴交于一定点![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号x | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款y(千亿元) | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于x的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数r的平方,当
恰好等于相关系数r的平方,当![]() 时,认为线性冋归模型是有效的,请计算
时,认为线性冋归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到0.001).
并且评价模型的拟合效果(计算结果精确到0.001).
附:
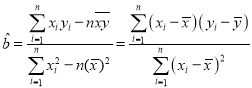 ,
,
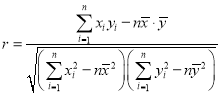
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】再直角坐标系中,定义两点![]() ,
,![]() 间的“直角距离”为
间的“直角距离”为![]() ,现有下列命题:
,现有下列命题:
①若![]() ,
,![]() 是
是![]() 轴上两点,则
轴上两点,则![]()
②已知![]() ,
,![]() ,则
,则![]() 为定值
为定值
③原点![]() 到直线
到直线![]() 上任一点
上任一点![]() 的直角距离
的直角距离![]() 的最小值为
的最小值为![]()
④设![]() 且
且![]() ,
,![]() ,若点
,若点![]() 是在过
是在过![]() 与
与![]() 的直线上,且点
的直线上,且点![]() 到点
到点![]() 与
与![]() 的“直角距离”之和等于
的“直角距离”之和等于![]() ,那么满足条件的点
,那么满足条件的点![]() 只有
只有![]() 个.
个.
其中的真命题是____________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个创业青年租用一块边长为4百米的等边![]() 田地
田地![]() 如图
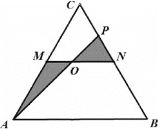
如图![]() 养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,
养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,![]() 规划在小路MN与AP的交点O(O与M、N不重合
规划在小路MN与AP的交点O(O与M、N不重合![]() 处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口
处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口![]() 小路的宽度不计
小路的宽度不计![]() 为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计
为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计![]() 为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
(Ⅰ)若拟修的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(Ⅱ)设![]() , 求
, 求![]() 的值,使得小路AO段与ON段的建造总费用最小.
的值,使得小路AO段与ON段的建造总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织高一年级学生到古都西安游学.在某景区,由于时间关系,每个班只能在甲、乙、丙三个景点中选择一个游览.高一![]() 班的
班的![]() 名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有
名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有![]() 人会选择甲,在乙、丙两个景点中有
人会选择甲,在乙、丙两个景点中有![]() 人会选择乙.那么关于这轮投票结果,下列说法正确的是
人会选择乙.那么关于这轮投票结果,下列说法正确的是
①该班选择去甲景点游览;
②乙景点的得票数可能会超过![]() ;
;
③丙景点的得票数不会比甲景点高;
④三个景点的得票数可能会相等.
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 在
在![]() 上是减函数;
上是减函数;
②![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
③![]() 在
在![]() 上至少有两个零点.
上至少有两个零点.
其中正确结论的序号为_________(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()

(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆![]() 的方程为:
的方程为:![]() ,
,![]() 为圆上任意一点,过
为圆上任意一点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,及直线
的最大值,及直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com