
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据导数几何意义得切线斜率等于![]() ,再根据点斜式求切线方程(2)先分离
,再根据点斜式求切线方程(2)先分离![]() 得
得![]() ,利用导数可得
,利用导数可得![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,因此
单调递减,因此![]() ,再根据单调性得
,再根据单调性得![]() ,最后根据零点存在定理可得a范围,根据a的取值范围可证不等式
,最后根据零点存在定理可得a范围,根据a的取值范围可证不等式
试题解析:(1)由已知条件, ![]() ,当
,当![]() 时,
时, ![]() ,
,
![]() ,当
,当![]() 时,
时, ![]() ,所以所求切线方程为
,所以所求切线方程为![]()
(2)由已知条件可得![]() 有两个相异实根
有两个相异实根![]() ,
,
令![]() ,则
,则![]() ,
,
1)若![]() ,则
,则![]() ,
, ![]() 单调递增,
单调递增, ![]() 不可能有两根;
不可能有两根;
2)若![]() ,
,
![]() 得
得![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
令![]() 解得
解得![]() ,
,
由![]() 有
有![]() ,
,
由![]() 有
有![]()
从而![]() 时函数
时函数![]() 有两个极值点
有两个极值点
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 |
| 单调递增 |
| 单调递减 |
因为![]() ,所以
,所以![]() ,
, ![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]()
另解:由已知可得![]() ,则
,则![]() ,令
,令![]() ,
,
则![]() ,可知函数
,可知函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
若![]() 有两个根,则可得
有两个根,则可得![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在锐角![]() 中,
中, ![]() 、
、![]() 、
、![]() 分别为角
分别为角![]() 、
、![]() 、
、![]() 所对的边,且
所对的边,且![]() .
.
(![]() )确定角
)确定角![]() 的大小.
的大小.
(![]() )若
)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]()
【解析】试题分析:(1)由正弦定理可知, ![]() ,所以
,所以![]() ;(2)由题意,
;(2)由题意, ![]() ,
, ![]() ,得到
,得到![]() .
.
试题解析:
(![]() )
)![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
17
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
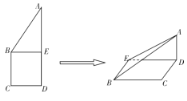
【题目】如图,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ;
;
③![]() 是
是![]() ;
;
④平面![]() 平面
平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为30°.
所成角为30°.
其中正确的有________.(填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,底面ABC为正三角形,
中,底面ABC为正三角形,![]() 底面ABC,
底面ABC,![]() ,点
,点![]() 在线段
在线段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)请指出点![]() 的位置,并给出证明;
的位置,并给出证明;
(2)若![]() ,求
,求![]() 与平面ABE夹角的正弦值.
与平面ABE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情期间,为了减少外出聚集,“线上买菜”受追捧.某电商平台在![]() 地区随机抽取了
地区随机抽取了![]() 位居民进行调研,获得了他们每个人近七天“线上买菜”消费总金额(单位:元),整理得到如图所示频率分布直方图.
位居民进行调研,获得了他们每个人近七天“线上买菜”消费总金额(单位:元),整理得到如图所示频率分布直方图.
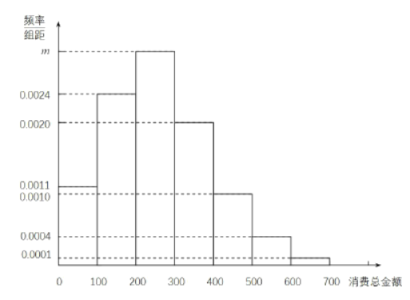
(1)求![]() 的值;
的值;
(2)从“线上买菜”消费总金额不低于![]() 元的被调研居民中,随机抽取
元的被调研居民中,随机抽取![]() 位给予奖品,求这
位给予奖品,求这![]() 位“线上买菜”消费总金额均低于
位“线上买菜”消费总金额均低于![]() 元的概率;
元的概率;
(3)若![]() 地区有
地区有![]() 万居民,该平台为了促进消费,拟对消费总金额不到平均水平一半的居民投放每人
万居民,该平台为了促进消费,拟对消费总金额不到平均水平一半的居民投放每人![]() 元的电子补贴.假设每组中的数据用该组区间的中点值代替,试根据上述频率分布直方图,估计该平台在
元的电子补贴.假设每组中的数据用该组区间的中点值代替,试根据上述频率分布直方图,估计该平台在![]() 地区拟投放的电子补贴总金额.
地区拟投放的电子补贴总金额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() .
.
(2)试问在棱![]() 上是否存在点
上是否存在点![]() ,使得面
,使得面![]() 面
面![]() ,若存在,试指出点
,若存在,试指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.

(1)求频率分布直方图中a的值;
(2)估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图估计20名学生数学考试成绩的众数,平均数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com