
【题目】已知数列{an}中,a1=2,a2=3,an>0,且满足an+12﹣an=an+1+an2(n∈N*).
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)设 ![]() (λ为正偶数,n∈N*),是否存在确定λ的值,使得对任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,说明理由.
(λ为正偶数,n∈N*),是否存在确定λ的值,使得对任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,说明理由.
【答案】
(1)解:由已知可得, ![]() ,且an>0,
,且an>0,
∴an+1﹣an=1(n∈N*),且a2﹣a1=1.
∴数列{an}是以a1=2为首项,公差为1的等差数列,
∴an=n+1
(2)解:由(1)知 ![]() ,
,
设它的前n项和为Tn
∴Tn=221+322+…+(n+1)2n,
2Tn=222+323+…+(n+1)2n+1,
两式相减可得: ![]()
所以 ![]()
(3)解:∵an=n+1,∴ ![]() ,
,
要使Cn+1>Cn恒成立,
则 ![]() 恒成立,
恒成立,
∴34n﹣λ2n+1>0恒成立,
∴λ<32n﹣1恒成立.
当且仅当n=1时,32n﹣1有最小值为3,∴λ<3.又λ为正偶数,则λ=2.
即存在λ=2,使得对任意n∈N*,都有Cn+1>Cn
【解析】(1)将条件化简可得an+1﹣an=1,再由等差数列的定义和通项公式,即可得到所求;(2)求得 ![]() ,再议数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和;(3)求得an=n+1,
,再议数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和;(3)求得an=n+1, ![]() ,要使Cn+1>Cn恒成立,运用作差法,再由参数分离,求得右边的最小值即可得到所求范围.
,要使Cn+1>Cn恒成立,运用作差法,再由参数分离,求得右边的最小值即可得到所求范围.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图象与直线l:y=﹣mx+n无公共点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1 , y1),B(x2 , y2)均在抛物线上. 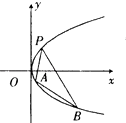
(1)求该抛物线方程;
(2)若AB的中点坐标为(1,﹣1),求直线AB方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求函数f(x)的极值;
(2)求证:当a>ln2﹣1且x>0时,ex>2x﹣2a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)经过点(1,
(a>b>0)经过点(1, ![]() ),且离心率等于
),且离心率等于 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(2,0)作直线PA,PB交椭圆于A,B两点,且满足PA⊥PB,试判断直线AB是否过定点,若过定点求出点坐标,若不过定点请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com