已知函数f(x)=x(1-x)2.
(1)求函数f(x)的极值;
(2)求实数a,b的值,使在区间[a,b]上的值域也为[a,b];.
(3)是否存在区间[a,0],使f(x)在区间[a,0]上的值域为[ka,0],且使k的值最小?若存在,求出k的最小值及此时a的值;若不存在,请说明理由.
分析:(1)对于三次函数:“f(x)=x(1-x)2.的极值问题利用其导数解决;
(2)三次函数的值域问题,往往转化为导数的问题,须针对最大值b与最小值a的取值情况进行讨论;
(3)对于存在性问题,先假设存在,然后转化为“封闭型”问题求解判断,若不出现矛盾,则肯定存在;若出现矛盾,则否定存在.
解答:解:(1)f(x)=x
3-2x
2+x,则f'(x)=3x
2-4x+1(1分)
令f'(x)=0解得:
x1=-1,x2=-,(2分)
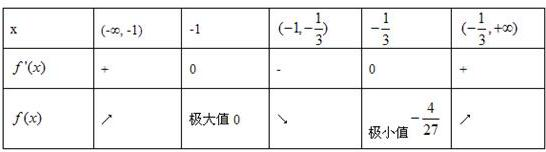
∴f(x)的极大值为f(-1)=0,极小值为
f(-)=-(4分)
(2)若最大值b与最小值a均在端点处取得,则有
或
(5分)
①当
时,则a,b即为方程f(x)=x的解,解得x
1=0,x
2=-2.
当-2≤x≤0时,-2≤f(x)≤0,检验知符合题意(6分)
②当
时,则有
相减得:(a-b)[a
2+(b+2)a+(b
2+2b+2)]=0.
又a≠b,而方程a
2+(b+2)a+(b
2+2b+2)=0中
△=(b+2)2-4(b2+2b+2)=-3(b+)2-<0,方程无解,故此时a,b不存在.
(8分)
若最大值b在区间(a,b)内取得,则b必为f(x)的极大值0,但b=0时f(b)=b,矛盾.
若最小值a在区间(a,b)内取得,则a必为f(x)的极小值
-,但f(x)在区间
[-,+∞)上单调递增,必有f(a)=a,矛盾.
综上得:a=-2,b=0(10分)
(3)易知k>0,
f(-)=-.
若f(a)=ka,则a(1+a)
2=ka即k=(1+a)
2,而此时
a≤-或-≤a<0.
当
-≤a<0时,
k=(1+a)2∈[,1),此时k有最小值为
.
当
a≤-时,
k=(1+a)2∈[,+∞),此时k有最小值
(12分)
若最小值ka在区间(a,0)内取得,则ka必为f(x)的极小值,即
ka=-,而此时
-<a<-,∴
<k<.
综上得:k的最小值为
,此时
a=-(14分)
点评:本题主要考查利用导数研究函数的极值,最值问题,以及存在性问题的解决方法,对于存在判断型问题,解题的策略一般为先假设存在,然后转化为“封闭型”问题求解判断,若不出现矛盾,则肯定存在;若出现矛盾,则否定存在.这是一种最常用也是最基本的方法.




 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<