
【题目】为了实现绿色发展,避免浪费能源,耨市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了20户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324.
对应的家庭收入数据如下:0.21,0.24,0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83,0.93,0.97,0.96,1.1,1.2,1.5,1.8.
(1)根据国家发改委的指示精神,该市计划实施3阶阶梯电价,使75%的用户在第一档,电价为0.56元/![]() ;
;![]() 的用户在第二档,电价为0.61元/
的用户在第二档,电价为0.61元/![]() ;
;![]() 的用户在第三档,电价为0.86元/
的用户在第三档,电价为0.86元/![]() ;试求出居民用电费用
;试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系式;
间的函数关系式;
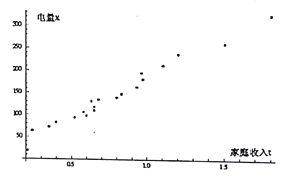
(2)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数)
的回归直线方程(回归直线方程的系数四舍五入保留整数)![]() ;
;
(3)小明家的月收入7000元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为.
的斜率和截距的最小二乘法估计分别为.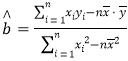 ,
,![]() ,其中
,其中![]() 为样本均值.
为样本均值.
【答案】(1) ;(2)
;(2)![]() ;(3)72.8.
;(3)72.8.
【解析】分析:(1)因为![]() ,
,
所以从用电量数据中得到第一档的临界值为第15个样本,即180,
第二档的临界值为第19个样本,即260.由此,可求居民用电费用![]() 与用电量
与用电量![]() 间的函数关系式;
间的函数关系式;
(2)计算可得![]() ,
,![]() ,代入公式可求
,代入公式可求![]() 关于
关于![]() 的回归直线方程
的回归直线方程
(3)把![]() 代入回归直线方程求出
代入回归直线方程求出![]() ,再把
,再把![]() 代入(1)函数解析式即可.
代入(1)函数解析式即可.
![]() ,所以,小明家月支出电费72.8元.
,所以,小明家月支出电费72.8元.
详解:(1)因为![]() ,
,
所以从用电量数据中得到第一档的临界值为第15个样本,即180,
第二档的临界值为第19个样本,即260.因此,
所以,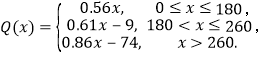
(2)由于![]() ,
,
![]() ,
,
 ,
,
所以![]() ,
,
从而回归直线方程为![]() .
.
(3)当![]() 时,
时,![]() ,
,
![]() ,所以,小明家月支出电费72.8元.
,所以,小明家月支出电费72.8元.


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 和
和![]() 是异面直线,
是异面直线,![]() 在平面
在平面![]() 内,
内,![]() 在平面
在平面![]() 内,
内,![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,则下列结论正确的是( )
的交线,则下列结论正确的是( )
A. ![]() 至少与
至少与![]() ,
,![]() 中的一条相交 B.
中的一条相交 B. ![]() 与
与![]() ,
,![]() 都不相交
都不相交
C. ![]() 与
与![]() ,
,![]() 都相交 D.
都相交 D. ![]() 至多与
至多与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业里工人的工资与其生产利润满足线性相关关系,现统计了100名工人的工资![]() (元)与其生产利润
(元)与其生产利润![]() (千元)的数据,建立了
(千元)的数据,建立了![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 工人甲的生产利润为1000元,则甲的工资为130元
B. 生产利润提高1000元,则预计工资约提高80元
C. 生产利润提高1000元,则预计工资约提高130元
D. 工人乙的工资为210元,则乙的生产利润为2000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com