
【题目】如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB=![]() ,SA=3,SB=5,
,SA=3,SB=5,![]() ,
,![]() ,
,![]() .
.
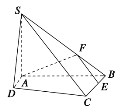
(1)求证:AB![]() 平面SAD;
平面SAD;
(2)求平面SCD与平面SAB所成的锐二面角的余弦值;
(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.
【答案】(1) 见解析;(2) ![]() ; (3)1
; (3)1
【解析】
(1)通过证明![]() ,
,![]() 得线面垂直;
得线面垂直;
(2)结合第一问结论,建立空间直角坐标系,求出两个平面的法向量,即可得二面角的余弦值;
(3)根据面面平行关系得出点F的位置,即可得到体积.
(1)证明:在![]() 中,因为
中,因为![]() ,
,
所以![]() .
.
又因为∠DAB=900
所以![]() ,
,
因为![]()
所以![]() 平面SAD.
平面SAD.
(2)解:因为 ![]() AD,
AD,![]() ,
,![]() ,
,
建立如图直角坐标系:

则A(0,0,0)B(0,4,0), C(2,4,0),D(1,0,0),S(0,0,3).
平面SAB的法向量为![]() .
.
设平面SDC的法向量为![]()
所以有
即![]() ,
,
令![]() ,
,
所以平面SDC的法向量为![]()
所以 .
.
(3)因为平面AEF//平面SCD,
平面AEF![]() 平面ABCD=AE,平面SCD
平面ABCD=AE,平面SCD![]() 平面ABCD=CD,
平面ABCD=CD,
所以![]() ,
,
平面AEF![]() 平面SBC=EF,平面SCD
平面SBC=EF,平面SCD![]() 平面SBC=SC,
平面SBC=SC,
所以![]()
由![]() ,AD//BC
,AD//BC
得四边形AEDC为平行四边形.
所以E为BC中点.
又![]() ,
,
所以F为SB中点.
所以F到平面ABE的距离为![]() ,
,
又![]() 的面积为2,
的面积为2,
所以![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知a,b是不相等的两个正数,在a,b之间插入两组实数:x1,x2,…,xn和y1,y2,…,yn,(n∈N*,且n≥2),使得a,x1,x2,…,xn,b成等差数列,a,y1,y2,…,yn,b成等比数列,给出下列四个式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定成立的是( )
.其中一定成立的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等差数列,a1=1,前n项和为Sn,数列{bn}为等比数列,b1>1,公比为2,且b2S3=54,b3+S2=16.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)设数列{cn}满足cn=an+bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的首项
的首项![]() ,数列
,数列![]() 前
前![]() 项和记为
项和记为![]() ,前
,前![]() 项积记为
项积记为![]() .
.
(1) 若![]() ,求等比数列
,求等比数列![]() 的公比
的公比![]() ;
;
(2) 在(1)的条件下,判断![]() 与
与![]() 的大小;并求
的大小;并求![]() 为何值时,
为何值时,![]() 取得最大值;
取得最大值;
(3) 在(1)的条件下,证明:若数列![]() 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为![]() ,则数列
,则数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,![]() ,点O为AD的中点,
,点O为AD的中点,![]() 且
且![]() .
.
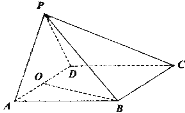
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求平面PBC与平面PAD所成二面角的正弦值.
,求平面PBC与平面PAD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log4(4x+1)+kx是偶函数.
(1)求k的值;
(2)判断函数y=f(x)-![]() x在R上的单调性,并加以证明;
x在R上的单调性,并加以证明;
(3)设g(x)=log4(a2x-![]() a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com