【题目】党的“十八大”之后，做好农业农村工作具有特殊重要的意义.国家为了更 好地服务于农民、开展社会主义新农村工作，派调查组到农村某地区考察.该地区有100户农 民，且都从事蔬菜种植.据了解，平均每户的年收入为6万元.为了调整产业结构，当地政府决 定动员部分农民从事蔬菜加工.据统计，若动员
户农民从事蔬菜加工，则剩下的继续 从事蔬菜种植的农民平均每户的年收入有望提高
，而从事蔬菜加工的农民平均每户的年收入为
万元.
（1）在动员
户农民从事蔬菜加工后，要使剩下
户从事蔬菜种植的所有农民总年收 入不低于动员前100户从事蔬菜种植的所有农民年总年收入，求
的取值范围；
（2）在（1）的条件下，要使这户农民从事蔬菜加工的总年收入始终不高于户从事蔬菜种植的所有农民年总年收入，求
的最大值.（参考数据：
)
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在
内,现将成绩按区间
,
,
,
，
进行分组,绘制成如下的频率分布直方图．
青年组
中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数；
(2)从青年组,的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自分数段的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题正确的是（ ）
A. 命题“若
，则
”的逆否命题为真命题；
B. 命题“
”为假命题，则命题
与命题
都是假命题；
C. “
”是“
”成立的必要不充分条件；
D. 命题“存在
，使得
”的否定是：“对任意
，均有
”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数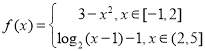
．
（1）在直角坐标系内直接画出
的图象；
（2）写出的单调区间，并指出单调性（不要求证明）；
（3）若函数
有两个不同的零点，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动圆
过定点
，并且内切于定圆
..
（1）求动圆圆心的轨迹方程；
（2）若
上存在两个点
，（1）中曲线上有两个点
，并且
三点共线，
三点共线，
，求四边形
的面积的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量（单位：万吨）的折线图.
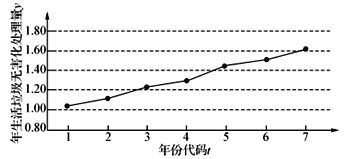
注：年份代码
分别表示对应年份
.
（1）由折线图看出，可用线性回归模型拟合
与
的关系，请用相关系数
（
线性相关较强）加以说明；
（2）建立与的回归方程(系数精确到0.01)，预测2019年该区生活垃圾无害化处理量.
（参考数据）
，
，
，
，
，
，
.
（参考公式）相关系数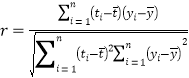
，在回归方程
中斜率和截距的最小二乘估计公式分别为：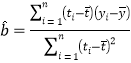
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
