
【题目】如图,在直三棱柱![]() 中,底面
中,底面![]() 为等边三角形,
为等边三角形, ![]() .
.
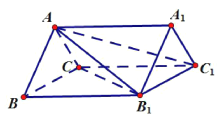
(Ⅰ)求三棱锥![]() 的体积;
的体积;
(Ⅱ)在线段![]() 上寻找一点
上寻找一点![]() ,使得
,使得![]() ,请说明作法和理由.
,请说明作法和理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)取BC中点E连结AE,三棱锥C1﹣CB1A的体积![]() ,由此能求出结果.(2)在矩形BB1C1C中,连结EC1,推导出Rt△C1CE∽Rt△CBF,从而CF⊥EC1,再求出AE⊥CF,由此得到在BB1上取F,使得
,由此能求出结果.(2)在矩形BB1C1C中,连结EC1,推导出Rt△C1CE∽Rt△CBF,从而CF⊥EC1,再求出AE⊥CF,由此得到在BB1上取F,使得![]() ,连结CF,CF即为所求直线.
,连结CF,CF即为所求直线.
解析:(1)取![]() 中点
中点![]() 连结
连结![]() .在等边三角形
.在等边三角形![]() 中,
中, ![]() ,
,
又∵在直三棱柱![]() 中,侧面
中,侧面![]() 面
面![]() ,
,
面![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() 为三棱锥
为三棱锥![]() 的高,又∵
的高,又∵![]() ,∴
,∴![]() ,
,
又∵底面![]() 为直角三角形,∴
为直角三角形,∴![]() ,
,
∴三棱锥![]() 的体积
的体积![]()
![]()
(2)作法:在![]() 上取
上取![]() ,使得
,使得![]() ,连结
,连结![]() ,
, ![]() 即为所求直线.
即为所求直线.
证明:如图,在矩形![]() 中,连结
中,连结![]() ,
,
∵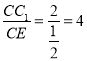 ,
, 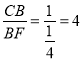 ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() 面
面![]() ,而
,而![]() 面
面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,∴
,∴![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(II)设![]() 为圆
为圆![]() 上的两个动点,
上的两个动点, ![]() ,若直线
,若直线![]() 和
和![]() 的斜率之积为定值2,试探求
的斜率之积为定值2,试探求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油![]() 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前![]() 个周需求量
个周需求量![]() 吨与
吨与![]() 的函数关系式为
的函数关系式为![]()
![]() ,
, ![]() 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.
(1)试写出第![]() 个周结束时,汽油存储量
个周结束时,汽油存储量![]() (吨)与
(吨)与![]() 的函数关系式;
的函数关系式;
(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)函数![]() 若存在
若存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数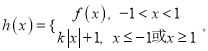 讨论函数
讨论函数![]() 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.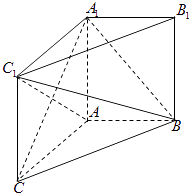
(Ⅰ)求证:A1C⊥平面ABC1;
(Ⅱ)求二面角A﹣BC1﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面材料:
根据两角和与差的正弦公式,有
![]() ------①
------①
![]() ------②
------②
由①+② 得![]() ------③
------③
令![]() 有
有![]()
代入③得![]() .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:
![]() ;
;
(Ⅱ)若![]() 的三个内角
的三个内角![]() 满足
满足![]() ,试判断
,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]() =λ(0<λ<1).
=λ(0<λ<1).
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆 ![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 ![]() 的焦点,且椭圆
的焦点,且椭圆 ![]() 的离心率是
的离心率是 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的动直线与椭圆
的动直线与椭圆 ![]() 相交于
相交于 ![]() 两点.若线段
两点.若线段 ![]() 的中点的横坐标是
的中点的横坐标是 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com