练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中e为自然对数的底数.

    （1）求证：函数是偶函数；

    （2）求证：函数在上单调递减；

    （3）求函数在闭区间上的最小值和最大值.

    【答案】（1）证明见解析（2）证明见解析（3）最小值为，最大值为

    【解析】

    （1）利用定义法证明是偶函数，注意定义域的分析；

    （2）利用定义法证明在上单调递减，注意函数单调性的证明步骤；

    （3）根据的单调性、奇偶性确定出在上的最值.

    （1）易知函数的定义域为R，显然关于原点对称.

    又因为，

    故根据偶函数的定义可知，函数是偶函数.

    （2）任取，且设，则

    .

    又由，得，所以；

    易知，

    所以，所以.

    于是，可得，

    即.

    故根据函数单调性的定义，可知函数在上单调递减.

    （3）根据（1）、（2）知函数的图象关于y轴对称，

    且在上单调递减，在上单调递增.

    据此易得函数在闭区间上的最小值为，最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知{xn}是各项均为正数的等比数列，且x1＋x2＝3，x3－x2＝2.

    (1)求数列{xn}的通项公式；

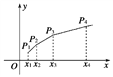
    (2)如图，在平面直角坐标系xOy中，依次连接点P1(x1,1)，P(x2,2)，…，Pn＋1(xn＋1，n＋1)得到折线P1P2…Pn＋1，求由该折线与直线y＝0，x＝x1，x＝xn＋1所围成的区域的面积Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

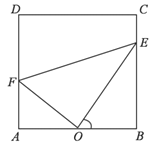
    【题目】某市为了改善居民的休闲娱乐活动场所，现有一块矩形草坪如下图所示，已知：米，米，拟在这块草坪内铺设三条小路、和，要求点是的中点，点在边上，点在边时上，且.

    （1）设，试求的周长关于的函数解析式，并求出此函数的定义域；

    （2）经核算，三条路每米铺设费用均为元，试问如何设计才能使铺路的总费用最低？并求出最低总费用.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为进一步贯彻落实“十九”大精神，某高校组织了“歌颂祖国，紧跟党走”为主题的党史知识竞赛,从参加竞赛的学生中，随机抽取40名学生，将其成绩分为六段，，，得到如图所示的频率分布直方图.

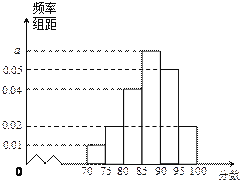
    （1）求图中的值；

    （2）若从竞赛成绩在与两个分数段的学生中随机选取两名学生，设这两名学生的竞赛成绩之差的绝对值不大于分为事件,求事件发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性 ；

    （2）若对任意恒成立，求实数的取值范围；

    （3）当时，若函数有两个极值点,求

    的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，函数的图像在处的切线方程为：

    （1）求的值；

    （2）若，成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，与均为边长是2的等边三角形，平面平面CBE，点O是BE的中点。

    （1）求证：；

    （2）求直线AB与平面ACE所成角的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3+ex-e-x．

    （1）判断此函数的奇偶性，并说明理由；

    （2）判断此函数的单调性（不需要证明）；

    （3）求不等式f（2x-1）+f（-3）＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是函数的部分图象.

    （1）求函数的表达式；

    （2）把函数的图象的周期扩大为原来的两倍，然后向右平移个单位，再把纵坐标伸长为原来的两倍，最后向上平移一个单位得到函数的图象.若对任意的，方程在区间上至多有一个解，求正数的取值范围.

    查看答案和解析>>

    同步练习册答案