
【题目】已知△ABC的三边长为a,b,c,则下列命题中真命题是( )
A.“a2+b2>c2”是“△ABC为锐角三角形”的充要条件
B.“a2+b2<c2”是“△ABC为钝角三角形”的必要不充分条件
C.“a3+b3=c3”是“△ABC为锐角三角形”的既不充分也不必要条件
D.“ ![]() +
+ ![]() =
= ![]() ”是“△ABC为钝角三角形”的充分不必要条件
”是“△ABC为钝角三角形”的充分不必要条件
【答案】C
【解析】解:若a2+b2>c2 , 由余弦定理可知cosC= ![]() >0,即角C为锐角,不能推出其他角均为锐角,故A为假命题; 若a2+b2<c2 , 由余弦定理可知cosC=
>0,即角C为锐角,不能推出其他角均为锐角,故A为假命题; 若a2+b2<c2 , 由余弦定理可知cosC= ![]() <0,则C为钝角,但若三角形为钝角三角形,钝角不一定是C,故“a2+b2<c2”是“△ABC为钝角三角形”的充分不必要条件,故B为假命题.
<0,则C为钝角,但若三角形为钝角三角形,钝角不一定是C,故“a2+b2<c2”是“△ABC为钝角三角形”的充分不必要条件,故B为假命题.
若 ![]() ,由余弦定理可知cosC=
,由余弦定理可知cosC= ![]() =0,则C为直角,故“
=0,则C为直角,故“ ![]() ”是“△ABC为钝角三角形”的即不充分也不必要条件,故D为假命题;
”是“△ABC为钝角三角形”的即不充分也不必要条件,故D为假命题;
a3+b3=c3”三角形即有锐角的可能,也有钝角的可能,故C为真命题.
故选C.
【考点精析】通过灵活运用余弦定理的定义,掌握余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(6,﹣3),
=(6,﹣3), ![]() =(5﹣x,﹣3﹣y),
=(5﹣x,﹣3﹣y), ![]() =(4,1)
=(4,1)
(1)若四边形ABCD是平行四边形,求x,y的值;
(2)若△ABC为等腰直角三角形,且∠B为直角,求x,y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求![]() 的值;
的值;
(2)已知![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(3)若![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入)
问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点. (Ⅰ)若 ![]() ,求直线AB的斜率;
,求直线AB的斜率;
(Ⅱ)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.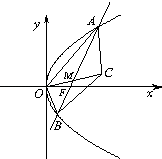
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017江西师范大学附属中学三模】已知函数![]() 是自然对数的底数).
是自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(Ⅰ)画出散点图;
(Ⅱ)求回归直线方程;
(Ⅲ)试预测广告费支出为10万元时,销售额多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com