
【题目】(1)求函数f(x)=![]() 的定义域 ,
的定义域 ,
(2)若当x![]() [-1,1]时,求函数f(x)=3x-2的值域.
[-1,1]时,求函数f(x)=3x-2的值域.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】某投资公司计划投资![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() ,
,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司现有100万元资金,并计划全部投入![]() 两种产品中,其中
两种产品中,其中![]() 万元资金投入
万元资金投入![]() 产品,试把
产品,试把![]() 两种产品利润总和
两种产品利润总和![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)怎样分配这100万元资金,才能使公司的利润总和![]() 获得最大?其最大利润总和为多少万元.
获得最大?其最大利润总和为多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
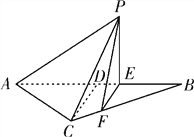
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() 的成员自驾时,自驾群体的人均通勤时间是
的成员自驾时,自驾群体的人均通勤时间是 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为40钟,根据上述分析结果回答下列问题:
影响,恒为40钟,根据上述分析结果回答下列问题:
(1)请你说明,当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C为锐角△ABC的三个内角,向量 ![]() =(2﹣2sinA,cosA+sinA),
=(2﹣2sinA,cosA+sinA), ![]() =(1+sinA,cosA﹣sinA),且
=(1+sinA,cosA﹣sinA),且 ![]() ⊥
⊥ ![]() .
.
(1)求A的大小;
(2)求y=2sin2B+cos( ![]() ﹣2B)取最大值时角B的大小.
﹣2B)取最大值时角B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com