
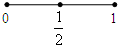
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
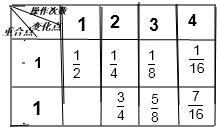
| 1 |
| 2n |
| 2n-1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 22 |
| 1 |
| 2n |
| 2n-1 |
| 2n |


科目:高中数学 来源: 题型:
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为查看答案和解析>>
科目:高中数学 来源: 题型:
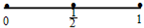 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=
(2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| j |
| 2n-2 |
| j |
| 2n-2 |
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二下学期第一次月考数学(文) 题型:选择题
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间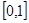 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标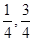 变成
变成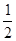 ,原来的坐标
,原来的坐标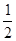 变成1,等等)。则区间
变成1,等等)。则区间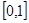 上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是
上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是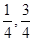 ,那么在第
,那么在第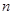 次操作完成后
次操作完成后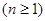 ,恰好被拉到与1重合的点对应的坐标是(
)
,恰好被拉到与1重合的点对应的坐标是(
)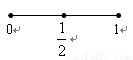
A.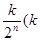 为
为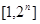 中所有奇数)
B.
中所有奇数)
B.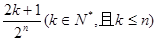
C.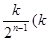 为
为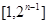 中所有奇数)
D.
中所有奇数)
D.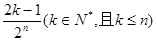
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com