
【题目】已知椭圆![]() 的一个焦点与短轴的两个端点是正三角形的三个项点,点
的一个焦点与短轴的两个端点是正三角形的三个项点,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)由题意可得![]() ,再把已知坐标代入椭圆方程,结合隐含条件求得
,再把已知坐标代入椭圆方程,结合隐含条件求得![]() 的值,即可求解椭圆
的值,即可求解椭圆![]() 的方程;(2)设出直线的方程,与椭圆方程联立,求出弦长及
的方程;(2)设出直线的方程,与椭圆方程联立,求出弦长及![]() 中点坐标,得到
中点坐标,得到![]() 所在的直线方程,再与椭圆方程联立,求得
所在的直线方程,再与椭圆方程联立,求得![]() 的坐标,分别化简
的坐标,分别化简![]() 和
和![]() ,即可证明结论.
,即可证明结论.
试题解析:(1)由已知,![]() ,又椭圆
,又椭圆![]() 过点
过点![]() ,
,
故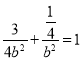 ,解得
,解得![]() ,∴
,∴![]() ,
,
所以椭圆![]() 的方程是
的方程是![]() ................................4分
................................4分
(2)设直线![]() 的方程为
的方程为![]() ,
,
由方程组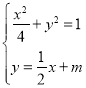 得
得![]() ,①
,①
方程① 的判别式为![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]() .
.
由①得![]() ..............................6分
..............................6分
所以![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 方程为
方程为![]() .
.
由方程组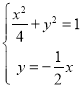 得
得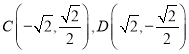 .........................8分
.........................8分
所以![]() ,
,
又![]()
![]() .
.
所以![]() ...........................................12分
...........................................12分


科目:高中数学 来源: 题型:
【题目】某企业准备投入适当的广告费对产品进行促销,在一年内预计销售量Q(万件)与广告费x(万元)之间的函数关系为Q=![]() (x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(1)试将年利润W(万元)表示为年广告费x(万元)的函数;(年利润=销售收入-成本)
(2)当年广告费为多少万元时,企业的年利润最大?最大年利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
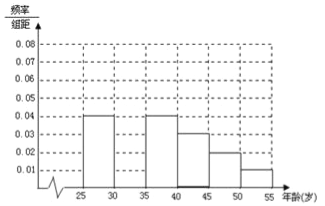
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)过(1)中轨迹![]() 上的点
上的点![]() 作两条直线分别与轨迹
作两条直线分别与轨迹![]() 相交于
相交于![]() 两点,试探究:当直线
两点,试探究:当直线![]() 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线![]() 的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com