
| 1 |
| f(n) |
| 1 |
| f(n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
| 1 |
| f(n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
| 2015 |
| 2016 |
| 2015 |
| 2016 |


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
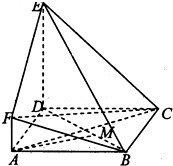 如图,ABCD是正方形,DE⊥平面ABCD.
如图,ABCD是正方形,DE⊥平面ABCD.| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为
在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com