
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴的 非负半轴为极轴建立极坐标系,曲线
轴的 非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)根据参数方程消去参数![]() 直接写出
直接写出![]() 的普通方程,利用
的普通方程,利用![]() 将
将![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)方法①:将![]() 的参数方程代入到
的参数方程代入到![]() 的直角坐标方程,根据
的直角坐标方程,根据![]() 的几何意义结合条件等式求解出
的几何意义结合条件等式求解出![]() 的值;
的值;
方法②:将![]() 的普通方程代入
的普通方程代入![]() 的直角坐标方程,根据韦达定理结合条件等式计算出
的直角坐标方程,根据韦达定理结合条件等式计算出![]() 的值即可.
的值即可.
(1)因为![]() 参数方程为
参数方程为![]() ,所以
,所以![]() 普通方程为:
普通方程为:![]() ,
,
因为![]() 的极坐标方程为
的极坐标方程为![]() ,所以
,所以![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)方法①:将曲线![]() 的参数方程化为
的参数方程化为 (
(![]() 为参数,
为参数,![]() ),
),
代入曲线![]() 得方程
得方程![]() ,
,
由![]() 得
得![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]() 把上式代入
把上式代入 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() ,
,
而![]() ,故
,故![]() 为所求;
为所求;
方法②:将曲线![]() 代入曲线
代入曲线![]() 得方程
得方程![]() ,
,
由![]() 得
得![]() ,
,
设方程的两个根分别为![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,![]() ,
,
由题意得![]() ,即
,即![]() ,
,
把![]() ,
,![]() 代入
代入![]() ,
,
所以![]() ,
,
化简得![]() ,解得
,解得![]() ,此为所求.
,此为所求.


科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
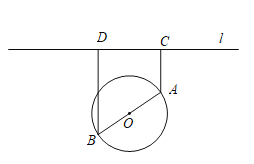
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
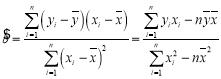 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )

A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com