
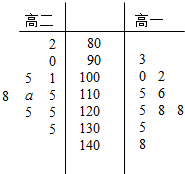
 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)分析 (1)由茎叶图能求出得小周在高三的10次数学考试成绩的中位数.
(2)(Ⅰ)由茎叶图得高二成绩中已有一个众数125,另有115,118,110+a,由此结合已知条件能求出茎叶图中a的值.
(Ⅱ)求出高三的平均成绩为119.高二时的10次数学考试成绩高于119分的有3个,由此能求出随机抽取茎叶图中的一个高二成绩,其分值高于高三成绩平均分的概率.
解答 解:(1)由茎叶图得小周在高三的10次数学考试成绩为:
93,100,102,115,116,125,128,128,135,148,
∴小周在高三的10次数学考试成绩的中位数为:$\frac{116+125}{2}$=120.5.
(2)(Ⅰ)由茎叶图得高二成绩中已有一个众数125,另有115,118,110+a,
∵茎叶阳中高二成绩栏内的数据恰有两个众数,
∴茎叶图中a的值为5或8.
(Ⅱ)高三的平均成绩为:
$\overline{x}$=$\frac{1}{10}$(93+100+102+115+116+125+128+128+135+148)=119.
高二时的10次数学考试成绩高于119分的有3个,
∴随机抽取茎叶图中的一个高二成绩,其分值高于高三成绩平均分的概率为p=$\frac{3}{10}$.
点评 本题考查中位数的求法,考查众数的概念,考查概率的求法,是基础题,解题时要认真审题,注意茎叶图的性质的合理运用.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
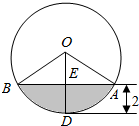 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 432 | B. | 540 | C. | 1377 | D. | 1620 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com