
【题目】已知函数y=f(x﹣1)的图象关于点(1,0)对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),若a=(30.3)f(30.3),b=(logπ3)f(logπ3),c=(log3 ![]() )f(log3
)f(log3 ![]() ),则 a,b,c的大小关系是( )
),则 a,b,c的大小关系是( )
A.a>b>c
B.c>a>b
C.c>b>a
D.a>c>b
【答案】B
【解析】解:∵当x∈(﹣∞,0)时不等式f(x)+xf′(x)<0成立,即:(xf(x))′<0,
∴xf(x)在 (﹣∞,0)上是减函数.
又∵函数y=f(x﹣1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
∴函数y=f(x)是定义在R上的奇函数
∴xf(x)是定义在R上的偶函数
∴xf(x)在 (0,+∞)上是增函数.
又∵30.3>1>log23>0> ![]() =﹣2,
=﹣2,
2=﹣ ![]() ,
,
∴(﹣ ![]() )f(﹣
)f(﹣ ![]() )>30.3f(30.3)>(logπ3)f(logπ3),即(
)>30.3f(30.3)>(logπ3)f(logπ3),即( ![]() )f(
)f( ![]() )>30.3f(30.3)>(logπ3)f(logπ3)
)>30.3f(30.3)>(logπ3)f(logπ3)
即:c>a>b
故选B.
【考点精析】根据题目的已知条件,利用函数单调性的性质和基本求导法则的相关知识可以得到问题的答案,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 ![]() 的中点.(12分)
的中点.(12分)
(Ⅰ)设P是 ![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.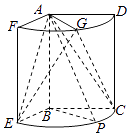
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名男生、3名女生站成一排:
(1)女生都不站在两端,有多少不同的站法?
(2)三名男生要相邻,有多少种不同的站法?
(3)三名女生互不相邻,三名男生也互不相邻,有多少种不同的站法?
(4)女生甲,女生乙都不与男生丙相邻,有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
![]()
(1)请根据表中提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度;(结果保留小数点后两位,参考数据:
的线性相关程度;(结果保留小数点后两位,参考数据: ![]() )
)
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式: ,
,![]() ;相关系数
;相关系数 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 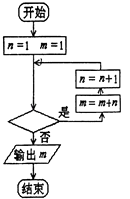
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(1)规定每日底薪50元,快递业务每完成一单提成3元;方案(2)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图。
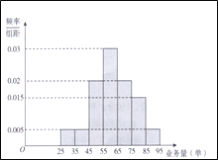
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案(1),丙、丁选择了日工资方案(2).现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案(1)的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com