
(13分)已知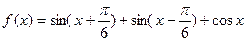
(1)求函数 的最小正周期;
的最小正周期;
(2)求 在区间
在区间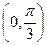 的值域。
的值域。
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)在平面直角坐标系 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角 ,
, ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 两点,已知
两点,已知 的纵坐标分别为
的纵坐标分别为 .(1)求
.(1)求 的值;(2)求
的值;(2)求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)(1)利用“五点法”画出函数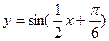 在长度为一个周期的闭
在长度为一个周期的闭
区间的简图
列表: 作图:
(2)并说明该函数图象可由y=sinx(x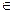 R)的图象经过怎样的变换得到。
R)的图象经过怎样的变换得到。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点, 线段MN经过△ABC的中心G,设Ð MGA=a(
MGA=a(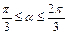 ).
). 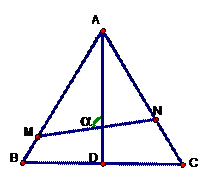
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数;
(2)求y=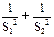 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com