
【题目】△ABC中,∠C=90°,M是BC的中点,若 ![]() ,则sin∠BAC= .
,则sin∠BAC= .
【答案】![]()
【解析】解:如图 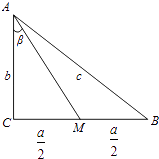
设AC=b,AB=c,CM=MB= ![]() ,∠MAC=β,
,∠MAC=β,
在△ABM中,由正弦定理可得 ![]() =
= ![]() ,
,
代入数据可得 ![]() =
= ![]() ,解得sin∠AMB=
,解得sin∠AMB= ![]() ,
,
故cosβ=cos( ![]() ﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB=
﹣∠AMC)=sin∠AMC=sin(π﹣∠AMB)=sin∠AMB= ![]() ,
,
而在RT△ACM中,cosβ= ![]() =
= ![]() ,
,
故可得 ![]() =
= ![]() ,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,
,化简可得a4﹣4a2b2+4b4=(a2﹣2b2)2=0,
解之可得a= ![]() b,再由勾股定理可得a2+b2=c2 , 联立可得c=
b,再由勾股定理可得a2+b2=c2 , 联立可得c= ![]() ,
,
故在RT△ABC中,sin∠BAC= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故答案为: ![]()
作出图象,设出未知量,在△ABM中,由正弦定理可得sin∠AMB= ![]() ,进而可得cosβ=
,进而可得cosβ= ![]() ,在RT△ACM中,还可得cosβ=
,在RT△ACM中,还可得cosβ= ![]() ,建立等式后可得a=
,建立等式后可得a= ![]() b,再由勾股定理可得c=
b,再由勾股定理可得c= ![]() ,而sin∠BAC═
,而sin∠BAC═ ![]() =
= ![]() ,代入化简可得答案.
,代入化简可得答案.


科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是边长为4的正方形,
是边长为4的正方形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)在图中作出并指明平面![]() 和平面
和平面![]() 的交线
的交线![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数f(x)=(ex﹣1)(x﹣1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取得极小值
B.当k=1时,f(x)在x=1处取得极大值
C.当k=2时,f(x)在x=1处取得极小值
D.当k=2时,f(x)在x=1处取得极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(Ⅰ)求出甲、乙所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() +
+ ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D. 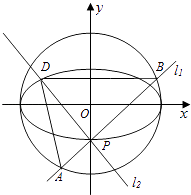
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率.
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“圆材埋壁”是《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,学会一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知道大小,用锯取锯它,锯口深一寸,锯道长一尺,问这块圆柱形木材的直径是多少?现有圆柱形木材一部分埋在墙壁中,截面如图所示,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,则阴影部分面积约为(注:
寸,则阴影部分面积约为(注:![]() ,
,![]() ,1尺=10寸)( )
,1尺=10寸)( )

A. 6.33平方寸B. 6.35平方寸
C. 6.37平方寸D. 6.39平方寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com