
分析 (1)利用二次函数的性质,函数的零点,列出不等式,即可求解m的范围.
(2)利用二次函数的对称轴以及函数的最值,列出不等式求解即可.
解答 解:(1)二次函数f(x)=x2+mx+3+2m,开口向上,
由图象可知$\left\{{\begin{array}{l}{f(0)<0}\\{f(5)<0}\end{array}}\right.$则m<-4 即 m∈(-∞,-4)…(6分)
(2)由题意可知$\left\{{\begin{array}{l}{-\frac{m}{2}<\frac{1+7}{2}}\\{f(7)=22}\end{array}}\right.$或$\left\{{\begin{array}{l}{-\frac{m}{2}≥4}\\{f(1)=22}\end{array}}\right.$
可得m=$-\frac{10}{3}$…(12分)(只要能够合理求出答案都给分)
点评 本题考查二次函数的性质的应用,考查计算能力,分类讨论思想的应用.


科目:高中数学 来源: 题型:解答题
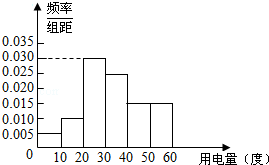 某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:| 分 组 | 频 数 | 频 率 |
| [0,10) | 0.05 | |
| [10,20) | 0.10 | |
| [20,30) | 30 | |
| [30,40) | 0.25 | |
| [40,50) | 0.15 | |
| [50,60] | 15 | |
| 合 计 | n | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (1,4) | C. | (-∞,-1)∪[4,+∞) | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com