
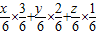 =
=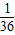 (3x+2y+z)
(3x+2y+z)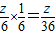 ,
,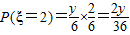
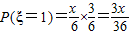 ,
,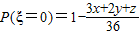
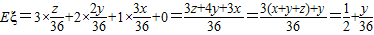
 ,此时x=z=0
,此时x=z=0

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学文 精华大字版 题型:044
同学A有一只放有x个红球、y个白球、z个黄球的箱子(x、y、z≥0,且x+y+z=6),同学B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
(Ⅰ)用x、y、z分别表示A胜与B胜的概率;
(Ⅱ)当A如何调整箱子中的球时,才能使自己获胜的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2008年浙江省宁波市镇海中学高考冲刺《概率与统计》系列训练(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com