
【题目】已知抛物线![]() :
:![]() 内有一点
内有一点![]() ,过
,过![]() 的两条直线
的两条直线![]() ,
,![]() 分别与抛物线
分别与抛物线![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 两点,且满足
两点,且满足![]() ,
,![]() ,已知线段
,已知线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
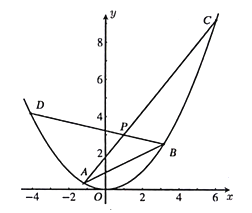
(1)求证:点![]() 的横坐标为定值;
的横坐标为定值;
(2)如果![]() ,点
,点![]() 的纵坐标小于3,求
的纵坐标小于3,求![]() 的面积的最大值.
的面积的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E为PC上一点,当F为DC的中点时,EF平行于平面PAD.
,E为PC上一点,当F为DC的中点时,EF平行于平面PAD.
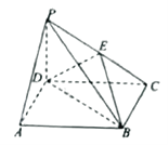
(Ⅰ)求证:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)写出抛物线![]() 的标准方程及其准线方程,并求抛物线
的标准方程及其准线方程,并求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)过点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(i)求点![]() 的坐标;
的坐标;
(ii)求![]() 与
与![]() 面积之和的最小值.
面积之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产,决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合结果,请完成以下任务:
.为了评价两种模型的拟合结果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 与
与![]() 的大小,判断哪个模型拟合效果更好;
的大小,判断哪个模型拟合效果更好;
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元.若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
参考公式: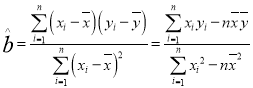 ,
,![]()
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是常数).
是常数).
(1)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(2)若![]() 为奇函数,求实数
为奇函数,求实数![]() .并证明
.并证明![]() 的图像始终在
的图像始终在![]() 的图像的下方;
的图像的下方;
(3)设函数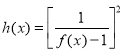 ,若对任意
,若对任意![]() ,以
,以![]() 为边长总可以构成三角形,求
为边长总可以构成三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
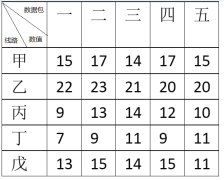
【题目】.华为公司研发的5G技术是中国在高科技领域的重大创新,目前处于世界领先地位,今年即将投入使用,它必将为人们生活带来别样的精彩,成为每个中国人的骄傲.现假设在一段光纤中有![]() 条通信线路,需要输送
条通信线路,需要输送![]() 种数据包,每条线路单位时间内输送不同数据包的大小数值如表所示.若在单位时间内,每条线路只能输送一种数据包,且使完成
种数据包,每条线路单位时间内输送不同数据包的大小数值如表所示.若在单位时间内,每条线路只能输送一种数据包,且使完成![]() 种数据包输送的数值总和最大,则下列叙述正确的序号是_______.
种数据包输送的数值总和最大,则下列叙述正确的序号是_______.
①甲线路只能输送第四种数据包;
②乙线路不能输送第二种数据包;
③丙线路可以不输送第三种数据包;
④丁线路可以输送第三种数据包;
⑤戊线路只能输送第四种数据包.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com