
【题目】正项数列{an}前n项和为Sn , 且 ![]() (n∈N+)
(n∈N+)
(1)求数列{an}的通项公式;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
【答案】
(1)解:依题意,当n=1时,a1=1;
当n≥2时,因为an>0, ![]() ,
,
所以 ![]() ,
,
两式相减,整理得:an﹣an﹣1=2,
所以数列{an}是以1为首项、2为公差的等差数列,
所以an=2n﹣1;
(2)证明:由(1)可知 ![]() ,
,
所以 ![]() ,
,
![]() ,
,
所以T2n﹣1>1>T2n(n∈N+)
【解析】(1)在 ![]() 中令n=1可知a1=1;当n≥2时,利用
中令n=1可知a1=1;当n≥2时,利用 ![]() 与
与 ![]() 作差,整理可知an﹣an﹣1=2,进而计算可得结论;(2)通过(1)裂项,分奇数、偶数两种情况讨论即可.
作差,整理可知an﹣an﹣1=2,进而计算可得结论;(2)通过(1)裂项,分奇数、偶数两种情况讨论即可.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系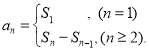 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择.
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(1)求某员工选择方案甲进行抽奖所奖金![]() (元)的分布列;
(元)的分布列;
(2)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设已知双曲线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,求
,求![]() ;
;
(2)若![]() ,椭圆
,椭圆![]() 上两个点
上两个点![]() 满足:
满足: ![]() 三点共线且
三点共线且![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
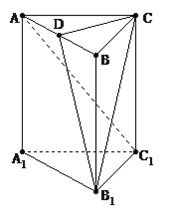
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 点D是AB的中点.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)线段AB上是否存在点M,使得A1M⊥平面CDB1?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传统文化就是文明演化而汇集成的一种反映民族特质和风貌的民族文化,是民族历史上各种思想文化、观念形态的总体表征.教育部考试中心确定了2017年普通高考部分学科更注重传统文化考核.某校为了了解高二年级中国数学传统文化选修课的教学效果,进行了一次阶段检测,并从中随机抽取80名同学的成绩,然后就其成绩分为![]() 五个等级进行数据统计如下:
五个等级进行数据统计如下:

根据以上抽样调查数据,视频率为概率.
(1)若该校高二年级共有1000名学生,试估算该校高二年级学生获得成绩为![]() 的人数;
的人数;
(2)若等级![]() 分别对应100分、80分、60分、40分、20分,学校要求“平均分达60分以上”为“教学达标”,请问该校高二年级此阶段教学是否达标?
分别对应100分、80分、60分、40分、20分,学校要求“平均分达60分以上”为“教学达标”,请问该校高二年级此阶段教学是否达标?
(3)为更深入了解教学情况,将成绩等级为![]() 的学生中,按分层抽样抽取7人,再从中任意抽取3名,求抽到成绩为
的学生中,按分层抽样抽取7人,再从中任意抽取3名,求抽到成绩为![]() 的人数
的人数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,已知AB=9,BC=6, ![]() =2
=2 ![]() .
.
(1)若四边形ABCD是矩形,求 ![]()
![]() 的值;
的值;
(2)若四边形ABCD是平行四边形,且 ![]()
![]() =6,求
=6,求 ![]() 与
与 ![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么
,那么![]() 平面
平面![]()
C. 不存在四个角都是直角的空间四边形
D. 空间图形经过中心投影后,直线还是直线,但平行直线可能变成相交的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 在区间
在区间![]() 上可被
上可被![]() 替代,
替代, ![]() 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②如果![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
③设![]() ,则存在实数
,则存在实数![]() 及区间
及区间![]() , 使得
, 使得![]() 在区间
在区间![]() 上被
上被![]() 替代.
替代.
其中真命题是
A. ①②③ B. ②③ C. ①③ D. ①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com